Hai M. Nguyen
Optimal Privacy Preserving in Wireless Federated Learning System over Mobile Edge Computing
Nov 14, 2022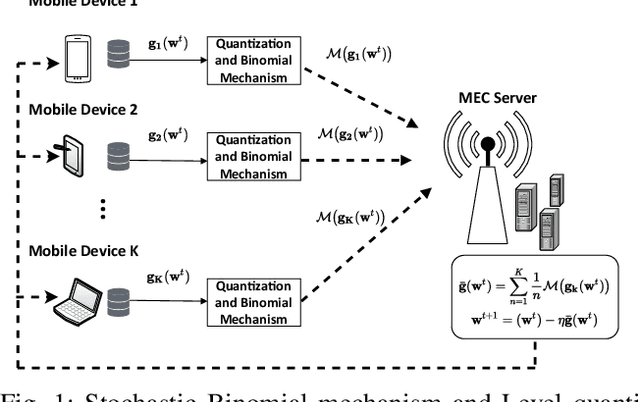
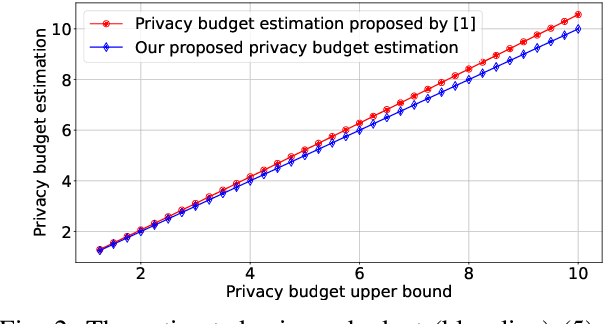
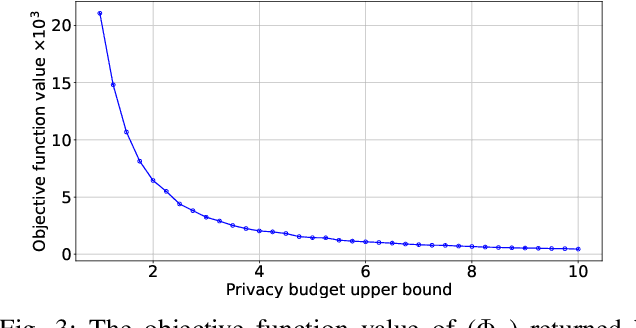
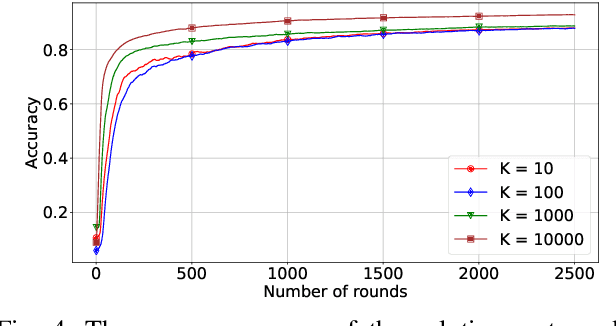
Abstract:Federated Learning (FL) with quantization and deliberately added noise over wireless networks is a promising approach to preserve the user differential privacy while reducing the wireless resources. Specifically, an FL learning process can be fused with quantized Binomial mechanism-based updates contributed by multiple users to reduce the communication overhead/cost as well as to protect the privacy of {participating} users. However, the optimization of wireless transmission and quantization parameters (e.g., transmit power, bandwidth, and quantization bits) as well as the added noise while guaranteeing the privacy requirement and the performance of the learned FL model remains an open and challenging problem. In this paper, we aim to jointly optimize the level of quantization, parameters of the Binomial mechanism, and devices' transmit powers to minimize the training time under the constraints of the wireless networks. The resulting optimization turns out to be a Mixed Integer Non-linear Programming (MINLP) problem, which is known to be NP-hard. To tackle it, we transform this MINLP problem into a new problem whose solutions are proved to be the optimal solutions of the original one. We then propose an approximate algorithm that can solve the transformed problem with an arbitrary relative error guarantee. Intensive simulations show that for the same wireless resources the proposed approach achieves the highest accuracy, close to that of the standard FL with no quantization and no noise added. This suggests the faster convergence/training time of the proposed wireless FL framework while optimally preserving users' privacy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge