Unified Representation Learning for Multi-Intent Diversity and Behavioral Uncertainty in Recommender Systems

This paper addresses the challenge of jointly modeling user intent diversity and behavioral uncertainty in recommender systems. A unified representation learning framework is proposed. The framework builds a multi-intent representation module and an uncertainty modeling mechanism. It extracts multi-granularity interest structures from user behavior sequences. Behavioral ambiguity and preference fluctuation are captured using Bayesian distribution modeling. In the multi-intent modeling part, the model introduces multiple latent intent vectors. These vectors are weighted and fused using an attention mechanism to generate semantically rich representations of long-term user preferences. In the uncertainty modeling part, the model learns the mean and covariance of behavior representations through Gaussian distributions. This reflects the user's confidence in different behavioral contexts. Next, a learnable fusion strategy is used to combine long-term intent and short-term behavior signals. This produces the final user representation, improving both recommendation accuracy and robustness. The method is evaluated on standard public datasets. Experimental results show that it outperforms existing representative models across multiple metrics. It also demonstrates greater stability and adaptability under cold-start and behavioral disturbance scenarios. The approach alleviates modeling bottlenecks faced by traditional methods when dealing with complex user behavior. These findings confirm the effectiveness and practical value of the unified modeling strategy in real-world recommendation tasks.

Locally Adaptive and Differentiable Regression

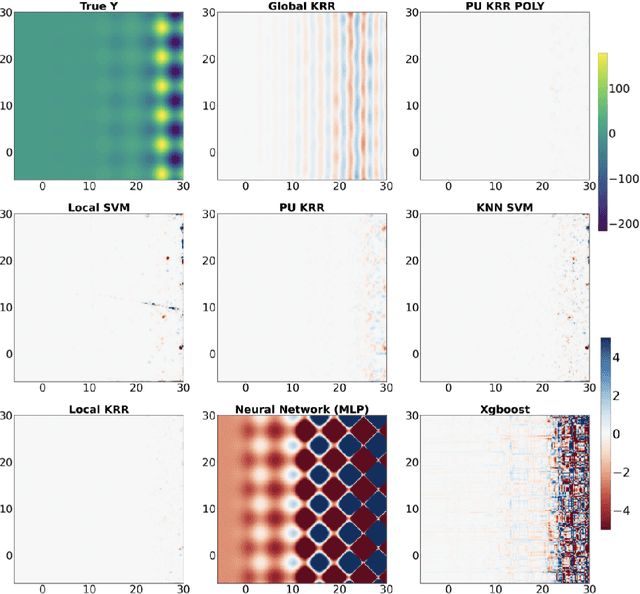
Over-parameterized models like deep nets and random forests have become very popular in machine learning. However, the natural goals of continuity and differentiability, common in regression models, are now often ignored in modern overparametrized, locally-adaptive models. We propose a general framework to construct a global continuous and differentiable model based on a weighted average of locally learned models in corresponding local regions. This model is competitive in dealing with data with different densities or scales of function values in different local regions. We demonstrate that when we mix kernel ridge and polynomial regression terms in the local models, and stitch them together continuously, we achieve faster statistical convergence in theory and improved performance in various practical settings.

The Kernel Spatial Scan Statistic

Kulldorff's (1997) seminal paper on spatial scan statistics (SSS) has led to many methods considering different regions of interest, different statistical models, and different approximations while also having numerous applications in epidemiology, environmental monitoring, and homeland security. SSS provides a way to rigorously test for the existence of an anomaly and provide statistical guarantees as to how "anomalous" that anomaly is. However, these methods rely on defining specific regions where the spatial information a point contributes is limited to binary 0 or 1, of either inside or outside the region, while in reality anomalies will tend to follow smooth distributions with decaying density further from an epicenter. In this work, we propose a method that addresses this shortcoming through a continuous scan statistic that generalizes SSS by allowing the point contribution to be defined by a kernel. We provide extensive experimental and theoretical results that shows our methods can be computed efficiently while providing high statistical power for detecting anomalous regions.