Approximate Maximum Halfspace Discrepancy

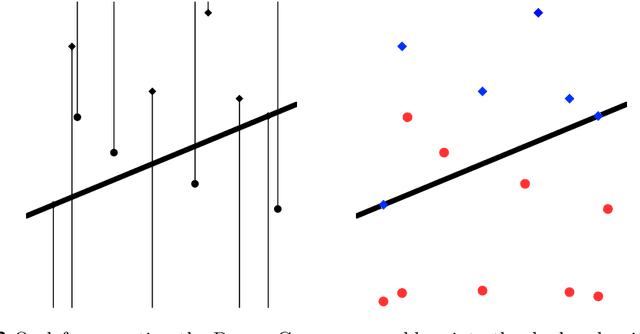
Consider the geometric range space $(X, \mathcal{H}_d)$ where $X \subset \mathbb{R}^d$ and $\mathcal{H}_d$ is the set of ranges defined by $d$-dimensional halfspaces. In this setting we consider that $X$ is the disjoint union of a red and blue set. For each halfspace $h \in \mathcal{H}_d$ define a function $\Phi(h)$ that measures the "difference" between the fraction of red and fraction of blue points which fall in the range $h$. In this context the maximum discrepancy problem is to find the $h^* = \arg \max_{h \in (X, \mathcal{H}_d)} \Phi(h)$. We aim to instead find an $\hat{h}$ such that $\Phi(h^*) - \Phi(\hat{h}) \le \varepsilon$. This is the central problem in linear classification for machine learning, in spatial scan statistics for spatial anomaly detection, and shows up in many other areas. We provide a solution for this problem in $O(|X| + (1/\varepsilon^d) \log^4 (1/\varepsilon))$ time, which improves polynomially over the previous best solutions. For $d=2$ we show that this is nearly tight through conditional lower bounds. For different classes of $\Phi$ we can either provide a $\Omega(|X|^{3/2 - o(1)})$ time lower bound for the exact solution with a reduction to APSP, or an $\Omega(|X| + 1/\varepsilon^{2-o(1)})$ lower bound for the approximate solution with a reduction to 3SUM. A key technical result is a $\varepsilon$-approximate halfspace range counting data structure of size $O(1/\varepsilon^d)$ with $O(\log (1/\varepsilon))$ query time, which we can build in $O(|X| + (1/\varepsilon^d) \log^4 (1/\varepsilon))$ time.

The Kernel Spatial Scan Statistic

Kulldorff's (1997) seminal paper on spatial scan statistics (SSS) has led to many methods considering different regions of interest, different statistical models, and different approximations while also having numerous applications in epidemiology, environmental monitoring, and homeland security. SSS provides a way to rigorously test for the existence of an anomaly and provide statistical guarantees as to how "anomalous" that anomaly is. However, these methods rely on defining specific regions where the spatial information a point contributes is limited to binary 0 or 1, of either inside or outside the region, while in reality anomalies will tend to follow smooth distributions with decaying density further from an epicenter. In this work, we propose a method that addresses this shortcoming through a continuous scan statistic that generalizes SSS by allowing the point contribution to be defined by a kernel. We provide extensive experimental and theoretical results that shows our methods can be computed efficiently while providing high statistical power for detecting anomalous regions.