Probabilistic Graph Circuits: Deep Generative Models for Tractable Probabilistic Inference over Graphs

Deep generative models (DGMs) have recently demonstrated remarkable success in capturing complex probability distributions over graphs. Although their excellent performance is attributed to powerful and scalable deep neural networks, it is, at the same time, exactly the presence of these highly non-linear transformations that makes DGMs intractable. Indeed, despite representing probability distributions, intractable DGMs deny probabilistic foundations by their inability to answer even the most basic inference queries without approximations or design choices specific to a very narrow range of queries. To address this limitation, we propose probabilistic graph circuits (PGCs), a framework of tractable DGMs that provide exact and efficient probabilistic inference over (arbitrary parts of) graphs. Nonetheless, achieving both exactness and efficiency is challenging in the permutation-invariant setting of graphs. We design PGCs that are inherently invariant and satisfy these two requirements, yet at the cost of low expressive power. Therefore, we investigate two alternative strategies to achieve the invariance: the first sacrifices the efficiency, and the second sacrifices the exactness. We demonstrate that ignoring the permutation invariance can have severe consequences in anomaly detection, and that the latter approach is competitive with, and sometimes better than, existing intractable DGMs in the context of molecular graph generation.

Sum-Product-Set Networks: Deep Tractable Models for Tree-Structured Graphs

Daily internet communication relies heavily on tree-structured graphs, embodied by popular data formats such as XML and JSON. However, many recent generative (probabilistic) models utilize neural networks to learn a probability distribution over undirected cyclic graphs. This assumption of a generic graph structure brings various computational challenges, and, more importantly, the presence of non-linearities in neural networks does not permit tractable probabilistic inference. We address these problems by proposing sum-product-set networks, an extension of probabilistic circuits from unstructured tensor data to tree-structured graph data. To this end, we use random finite sets to reflect a variable number of nodes and edges in the graph and to allow for exact and efficient inference. We demonstrate that our tractable model performs comparably to various intractable models based on neural networks.

GraphSPNs: Sum-Product Networks Benefit From Canonical Orderings

Deep generative models have recently made a remarkable progress in capturing complex probability distributions over graphs. However, they are intractable and thus unable to answer even the most basic probabilistic inference queries without resorting to approximations. Therefore, we propose graph sum-product networks (GraphSPNs), a tractable deep generative model which provides exact and efficient inference over (arbitrary parts of) graphs. We investigate different principles to make SPNs permutation invariant. We demonstrate that GraphSPNs are able to (conditionally) generate novel and chemically valid molecular graphs, being competitive to, and sometimes even better than, existing intractable models. We find out that (Graph)SPNs benefit from ensuring the permutation invariance via canonical ordering.

Sum-Product-Set Networks

Daily internet communication relies heavily on tree-structured graphs, embodied by popular data formats such as XML and JSON. However, many recent generative (probabilistic) models utilize neural networks to learn a probability distribution over undirected cyclic graphs. This assumption of a generic graph structure brings various computational challenges, and, more importantly, the presence of non-linearities in neural networks does not permit tractable probabilistic inference. We address these problems by proposing sum-product-set networks, an extension of probabilistic circuits from unstructured tensor data to tree-structured graph data. To this end, we use random finite sets to reflect a variable number of nodes and edges in the graph and to allow for exact and efficient inference. We demonstrate that our tractable model performs comparably to various intractable models based on neural networks.

Fitting large mixture models using stochastic component selection

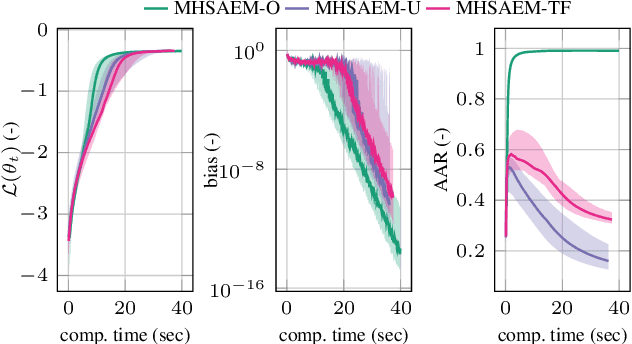
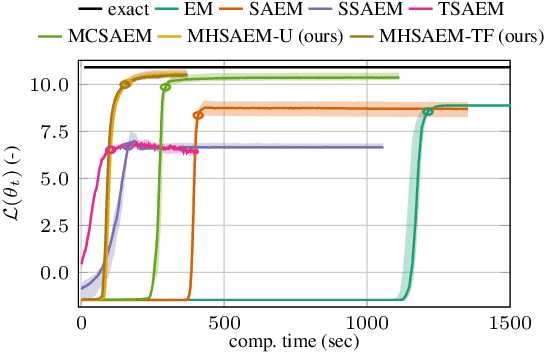
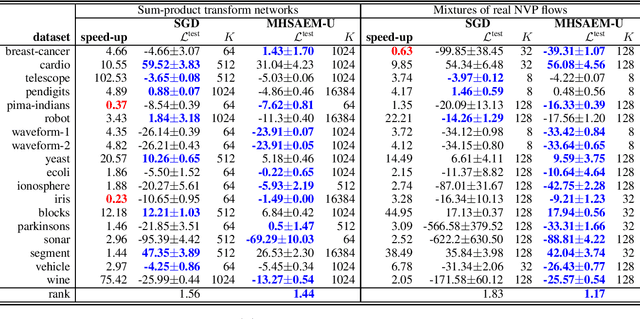
Traditional methods for unsupervised learning of finite mixture models require to evaluate the likelihood of all components of the mixture. This becomes computationally prohibitive when the number of components is large, as it is, for example, in the sum-product (transform) networks. Therefore, we propose to apply a combination of the expectation maximization and the Metropolis-Hastings algorithm to evaluate only a small number of, stochastically sampled, components, thus substantially reducing the computational cost. The Markov chain of component assignments is sequentially generated across the algorithm's iterations, having a non-stationary target distribution whose parameters vary via a gradient-descent scheme. We put emphasis on generality of our method, equipping it with the ability to train both shallow and deep mixture models which involve complex, and possibly nonlinear, transformations. The performance of our method is illustrated in a variety of synthetic and real-data contexts, considering deep models, such as mixtures of normalizing flows and sum-product (transform) networks.

Transferring model structure in Bayesian transfer learning for Gaussian process regression

Bayesian transfer learning (BTL) is defined in this paper as the task of conditioning a target probability distribution on a transferred source distribution. The target globally models the interaction between the source and target, and conditions on a probabilistic data predictor made available by an independent local source modeller. Fully probabilistic design is adopted to solve this optimal decision-making problem in the target. By successfully transferring higher moments of the source, the target can reject unreliable source knowledge (i.e. it achieves robust transfer). This dual-modeller framework means that the source's local processing of raw data into a transferred predictive distribution -- with compressive possibilities -- is enriched by (the possible expertise of) the local source model. In addition, the introduction of the global target modeller allows correlation between the source and target tasks -- if known to the target -- to be accounted for. Important consequences emerge. Firstly, the new scheme attains the performance of fully modelled (i.e. conventional) multitask learning schemes in (those rare) cases where target model misspecification is avoided. Secondly, and more importantly, the new dual-modeller framework is robust to the model misspecification that undermines conventional multitask learning. We thoroughly explore these issues in the key context of interacting Gaussian process regression tasks. Experimental evidence from both synthetic and real data settings validates our technical findings: that the proposed BTL framework enjoys robustness in transfer while also being robust to model misspecification.