Probabilistic Graph Circuits: Deep Generative Models for Tractable Probabilistic Inference over Graphs
Paper and Code
Mar 15, 2025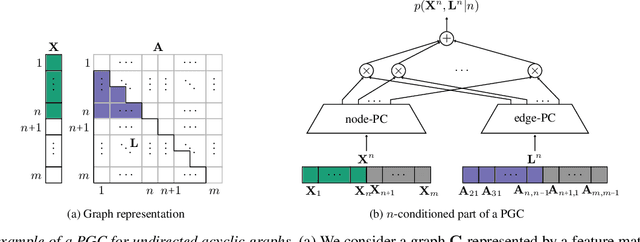
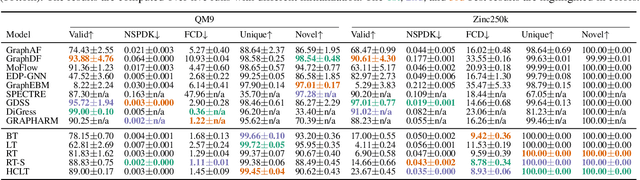
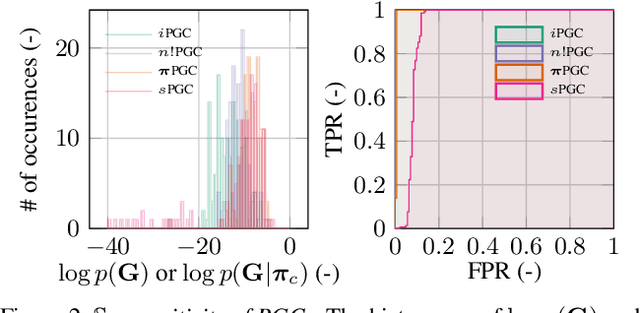
Deep generative models (DGMs) have recently demonstrated remarkable success in capturing complex probability distributions over graphs. Although their excellent performance is attributed to powerful and scalable deep neural networks, it is, at the same time, exactly the presence of these highly non-linear transformations that makes DGMs intractable. Indeed, despite representing probability distributions, intractable DGMs deny probabilistic foundations by their inability to answer even the most basic inference queries without approximations or design choices specific to a very narrow range of queries. To address this limitation, we propose probabilistic graph circuits (PGCs), a framework of tractable DGMs that provide exact and efficient probabilistic inference over (arbitrary parts of) graphs. Nonetheless, achieving both exactness and efficiency is challenging in the permutation-invariant setting of graphs. We design PGCs that are inherently invariant and satisfy these two requirements, yet at the cost of low expressive power. Therefore, we investigate two alternative strategies to achieve the invariance: the first sacrifices the efficiency, and the second sacrifices the exactness. We demonstrate that ignoring the permutation invariance can have severe consequences in anomaly detection, and that the latter approach is competitive with, and sometimes better than, existing intractable DGMs in the context of molecular graph generation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge