Generalization of Auto-Regressive Hidden Markov Models to Non-Linear Dynamics and Non-Euclidean Observation Space

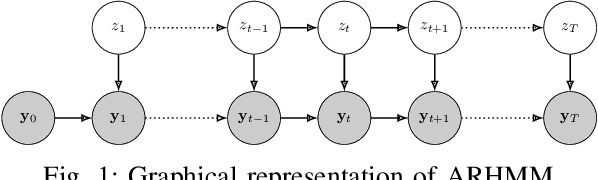
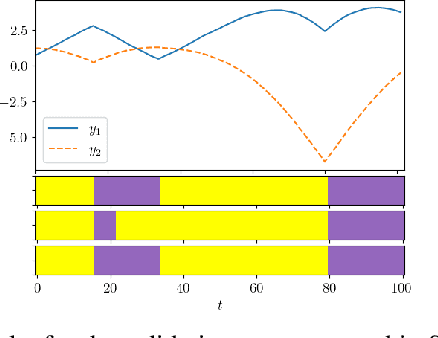
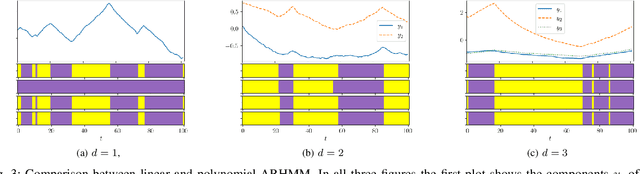
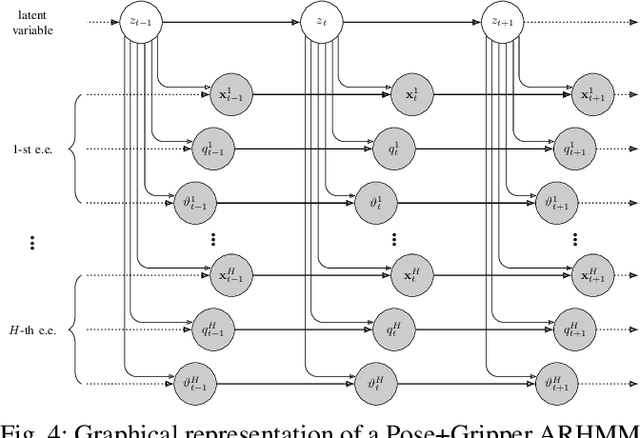
Latent variable models are widely used to perform unsupervised segmentation of time series in different context such as robotics, speech recognition, and economics. One of the most widely used latent variable model is the Auto-Regressive Hidden Markov Model (ARHMM), which combines a latent mode governed by a Markov chain dynamics with a linear Auto-Regressive dynamics of the observed state. In this work, we propose two generalizations of the ARHMM. First, we propose a more general AR dynamics in Cartesian space, described as a linear combination of non-linear basis functions. Second, we propose a linear dynamics in unit quaternion space, in order to properly describe orientations. These extensions allow to describe more complex dynamics of the observed state. Although this extension is proposed for the ARHMM, it can be easily extended to other latent variable models with AR dynamics in the observed space, such as Auto-Regressive Hidden semi-Markov Models.

Dynamic Movement Primitives: Volumetric Obstacle Avoidance Using Dynamic Potential Functions

Obstacle avoidance for DMPs is still a challenging problem. In our previous work, we proposed a framework for obstacle avoidance based on superquadric potential functions to represent volumes. In this work, we extend our previous work to include the velocity of the trajectory in the definition of the potential. Our formulations guarantee smoother behavior with respect to state-of-the-art point-like methods. Moreover, our new formulation allows to obtain a smoother behavior in proximity of the obstacle than when using a static (i.e. velocity independent) potential. We validate our framework for obstacle avoidance in a simulated multi-robot scenario and with different real robots: a pick-and-place task for an industrial manipulator and a surgical robot to show scalability; and navigation with a mobile robot in dynamic environment.

Autonomous task planning and situation awareness in robotic surgery

The use of robots in minimally invasive surgery has improved the quality of standard surgical procedures. So far, only the automation of simple surgical actions has been investigated by researchers, while the execution of structured tasks requiring reasoning on the environment and the choice among multiple actions is still managed by human surgeons. In this paper, we propose a framework to implement surgical task automation. The framework consists of a task-level reasoning module based on answer set programming, a low-level motion planning module based on dynamic movement primitives, and a situation awareness module. The logic-based reasoning module generates explainable plans and is able to recover from failure conditions, which are identified and explained by the situation awareness module interfacing to a human supervisor, for enhanced safety. Dynamic Movement Primitives allow to replicate the dexterity of surgeons and to adapt to obstacles and changes in the environment. The framework is validated on different versions of the standard surgical training peg-and-ring task.

DMP++: Overcoming Some Drawbacks of Dynamic Movement Primitives

Dynamic Movement Primitives (DMPs) is a framework for learning a point-to-point trajectory from a demonstration. Despite being widely used, DMPs still present some shortcomings that may limit their usage in real robotic applications. Firstly, adaptation of the trajectory generated by the DMP heavily depends on the choice of hyperparameters and on the new desired goal position. Secondly, DMPs are a framework for `one-shot learning', meaning that they are limited to learn from a unique demonstration. In this work, we propose a technique to make the generalization of the trajectory robust against the choice of hyperparameters and new goal positions. Moreover, we also propose a strategy to extract a common behavior from multiple observations. We also present a new set of basis functions to be used in the learning process.