Generalization of Auto-Regressive Hidden Markov Models to Non-Linear Dynamics and Non-Euclidean Observation Space

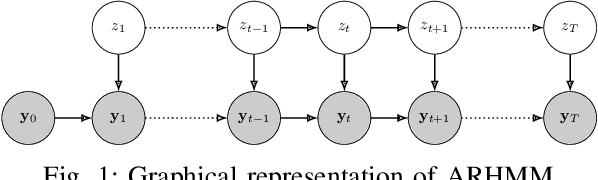
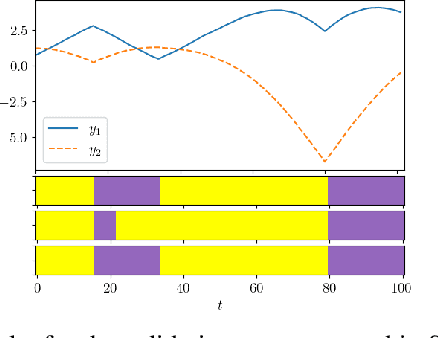
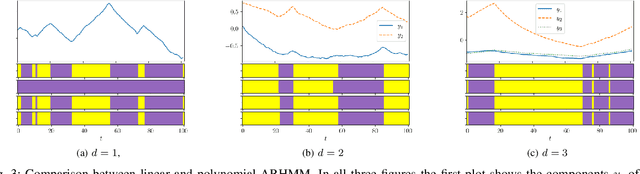
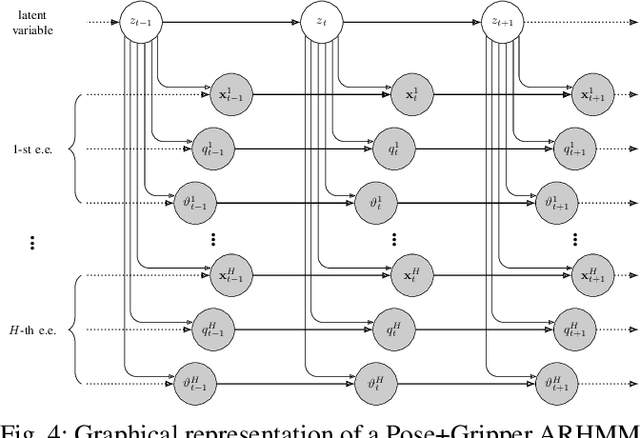
Latent variable models are widely used to perform unsupervised segmentation of time series in different context such as robotics, speech recognition, and economics. One of the most widely used latent variable model is the Auto-Regressive Hidden Markov Model (ARHMM), which combines a latent mode governed by a Markov chain dynamics with a linear Auto-Regressive dynamics of the observed state. In this work, we propose two generalizations of the ARHMM. First, we propose a more general AR dynamics in Cartesian space, described as a linear combination of non-linear basis functions. Second, we propose a linear dynamics in unit quaternion space, in order to properly describe orientations. These extensions allow to describe more complex dynamics of the observed state. Although this extension is proposed for the ARHMM, it can be easily extended to other latent variable models with AR dynamics in the observed space, such as Auto-Regressive Hidden semi-Markov Models.