Memory-Aware Social Learning under Partial Information Sharing

This work examines a social learning problem, where dispersed agents connected through a network topology interact locally to form their opinions (beliefs) as regards certain hypotheses of interest. These opinions evolve over time, since the agents collect observations from the environment, and update their current beliefs by accounting for: their past beliefs, the innovation contained in the new data, and the beliefs received from the neighbors. The distinguishing feature of the present work is that agents are constrained to share opinions regarding only a single hypothesis. We devise a novel learning strategy where each agent forms a valid belief by completing the partial beliefs received from its neighbors. This completion is performed by exploiting the knowledge accumulated in the past beliefs, thanks to a principled memory-aware rule inspired by a Bayesian criterion. The analysis allows us to characterize the role of memory in social learning under partial information sharing, revealing novel and nontrivial learning dynamics. Surprisingly, we establish that the standard classification rule based on selecting the maximum belief is not optimal under partial information sharing, while there exists a consistent threshold-based decision rule that allows each agent to classify correctly the hypothesis of interest. We also show that the proposed strategy outperforms previously considered schemes, highlighting that the introduction of memory in the social learning algorithm is critical to overcome the limitations arising from sharing partial information.

On the Stability and Generalization of Learning with Kernel Activation Functions

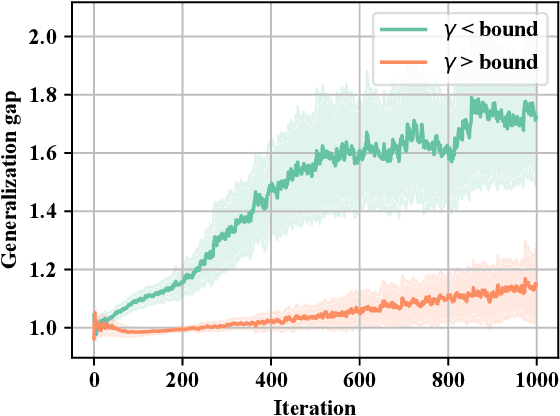
In this brief we investigate the generalization properties of a recently-proposed class of non-parametric activation functions, the kernel activation functions (KAFs). KAFs introduce additional parameters in the learning process in order to adapt nonlinearities individually on a per-neuron basis, exploiting a cheap kernel expansion of every activation value. While this increase in flexibility has been shown to provide significant improvements in practice, a theoretical proof for its generalization capability has not been addressed yet in the literature. Here, we leverage recent literature on the stability properties of non-convex models trained via stochastic gradient descent (SGD). By indirectly proving two key smoothness properties of the models under consideration, we prove that neural networks endowed with KAFs generalize well when trained with SGD for a finite number of steps. Interestingly, our analysis provides a guideline for selecting one of the hyper-parameters of the model, the bandwidth of the scalar Gaussian kernel. A short experimental evaluation validates the proof.