The Pseudo-Dimension of Contracts

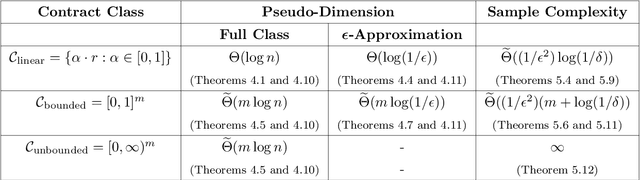
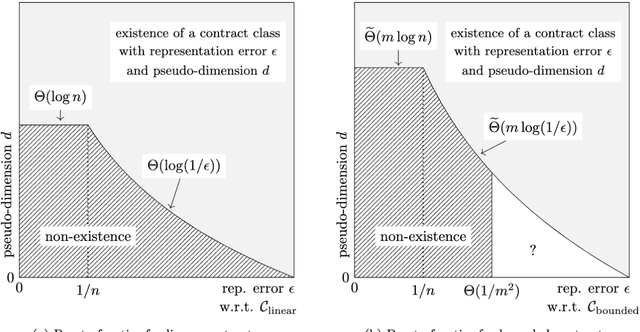
Algorithmic contract design studies scenarios where a principal incentivizes an agent to exert effort on her behalf. In this work, we focus on settings where the agent's type is drawn from an unknown distribution, and formalize an offline learning framework for learning near-optimal contracts from sample agent types. A central tool in our analysis is the notion of pseudo-dimension from statistical learning theory. Beyond its role in establishing upper bounds on the sample complexity, pseudo-dimension measures the intrinsic complexity of a class of contracts, offering a new perspective on the tradeoffs between simplicity and optimality in contract design. Our main results provide essentially optimal tradeoffs between pseudo-dimension and representation error (defined as the loss in principal's utility) with respect to linear and bounded contracts. Using these tradeoffs, we derive sample- and time-efficient learning algorithms, and demonstrate their near-optimality by providing almost matching lower bounds on the sample complexity. Conversely, for unbounded contracts, we prove an impossibility result showing that no learning algorithm exists. Finally, we extend our techniques in three important ways. First, we provide refined pseudo-dimension and sample complexity guarantees for the combinatorial actions model, revealing a novel connection between the number of critical values and sample complexity. Second, we extend our results to menus of contracts, showing that their pseudo-dimension scales linearly with the menu size. Third, we adapt our algorithms to the online learning setting, where we show that, a polynomial number of type samples suffice to learn near-optimal bounded contracts. Combined with prior work, this establishes a formal separation between expert advice and bandit feedback for this setting.

On Voting and Facility Location

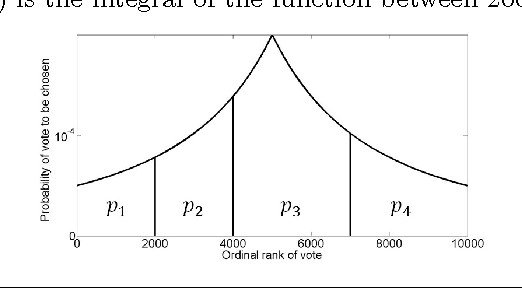
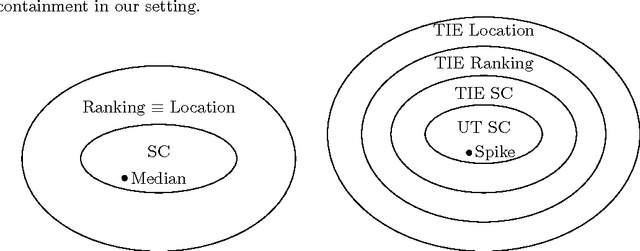
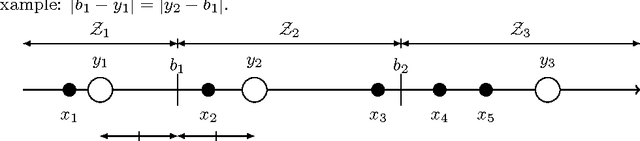
We study mechanisms for candidate selection that seek to minimize the social cost, where voters and candidates are associated with points in some underlying metric space. The social cost of a candidate is the sum of its distances to each voter. Some of our work assumes that these points can be modeled on a real line, but other results of ours are more general. A question closely related to candidate selection is that of minimizing the sum of distances for facility location. The difference is that in our setting there is a fixed set of candidates, whereas the large body of work on facility location seems to consider every point in the metric space to be a possible candidate. This gives rise to three types of mechanisms which differ in the granularity of their input space (voting, ranking and location mechanisms). We study the relationships between these three classes of mechanisms. While it may seem that Black's 1948 median algorithm is optimal for candidate selection on the line, this is not the case. We give matching upper and lower bounds for a variety of settings. In particular, when candidates and voters are on the line, our universally truthful spike mechanism gives a [tight] approximation of two. When assessing candidate selection mechanisms, we seek several desirable properties: (a) efficiency (minimizing the social cost) (b) truthfulness (dominant strategy incentive compatibility) and (c) simplicity (a smaller input space). We quantify the effect that truthfulness and simplicity impose on the efficiency.

Solving Cooperative Reliability Games

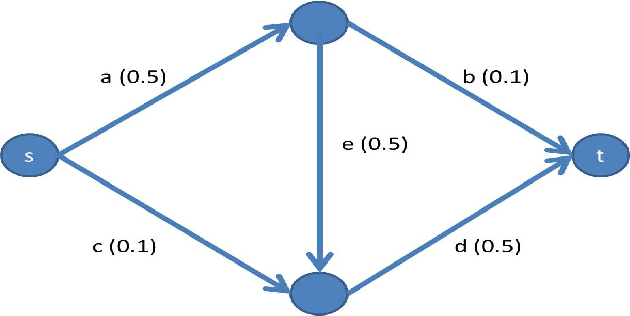
Cooperative games model the allocation of profit from joint actions, following considerations such as stability and fairness. We propose the reliability extension of such games, where agents may fail to participate in the game. In the reliability extension, each agent only "survives" with a certain probability, and a coalition's value is the probability that its surviving members would be a winning coalition in the base game. We study prominent solution concepts in such games, showing how to approximate the Shapley value and how to compute the core in games with few agent types. We also show that applying the reliability extension may stabilize the game, making the core non-empty even when the base game has an empty core.