An $α$-regret analysis of Adversarial Bilateral Trade

We study sequential bilateral trade where sellers and buyers valuations are completely arbitrary (i.e., determined by an adversary). Sellers and buyers are strategic agents with private valuations for the good and the goal is to design a mechanism that maximizes efficiency (or gain from trade) while being incentive compatible, individually rational and budget balanced. In this paper we consider gain from trade which is harder to approximate than social welfare. We consider a variety of feedback scenarios and distinguish the cases where the mechanism posts one price and when it can post different prices for buyer and seller. We show several surprising results about the separation between the different scenarios. In particular we show that (a) it is impossible to achieve sublinear $\alpha$-regret for any $\alpha<2$, (b) but with full feedback sublinear $2$-regret is achievable (c) with a single price and partial feedback one cannot get sublinear $\alpha$ regret for any constant $\alpha$ (d) nevertheless, posting two prices even with one-bit feedback achieves sublinear $2$-regret, and (e) there is a provable separation in the $2$-regret bounds between full and partial feedback.

On Voting and Facility Location

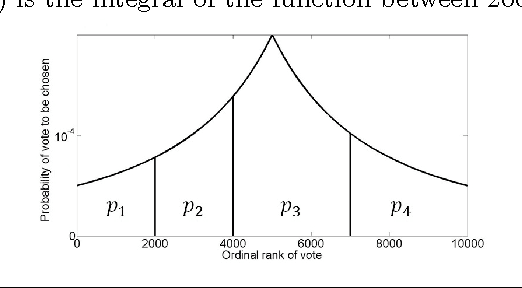
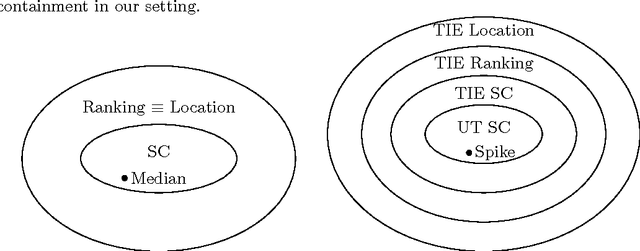
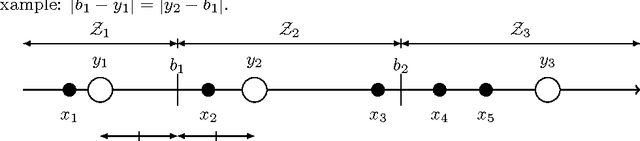
We study mechanisms for candidate selection that seek to minimize the social cost, where voters and candidates are associated with points in some underlying metric space. The social cost of a candidate is the sum of its distances to each voter. Some of our work assumes that these points can be modeled on a real line, but other results of ours are more general. A question closely related to candidate selection is that of minimizing the sum of distances for facility location. The difference is that in our setting there is a fixed set of candidates, whereas the large body of work on facility location seems to consider every point in the metric space to be a possible candidate. This gives rise to three types of mechanisms which differ in the granularity of their input space (voting, ranking and location mechanisms). We study the relationships between these three classes of mechanisms. While it may seem that Black's 1948 median algorithm is optimal for candidate selection on the line, this is not the case. We give matching upper and lower bounds for a variety of settings. In particular, when candidates and voters are on the line, our universally truthful spike mechanism gives a [tight] approximation of two. When assessing candidate selection mechanisms, we seek several desirable properties: (a) efficiency (minimizing the social cost) (b) truthfulness (dominant strategy incentive compatibility) and (c) simplicity (a smaller input space). We quantify the effect that truthfulness and simplicity impose on the efficiency.