Reduce, Reuse, Recycle: Categories for Compositional Reinforcement Learning

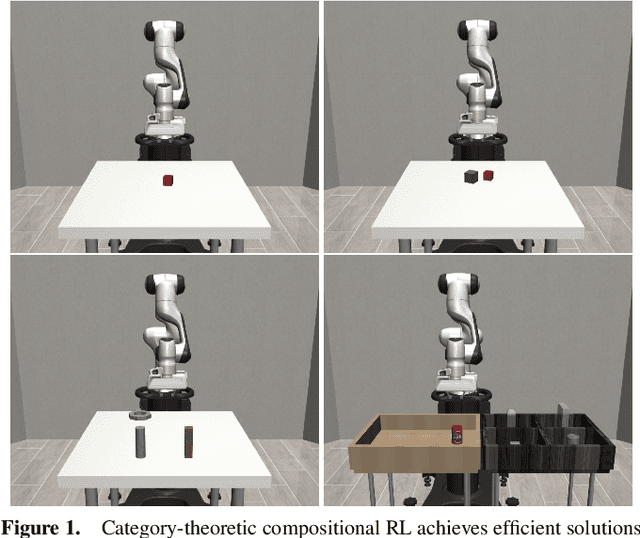
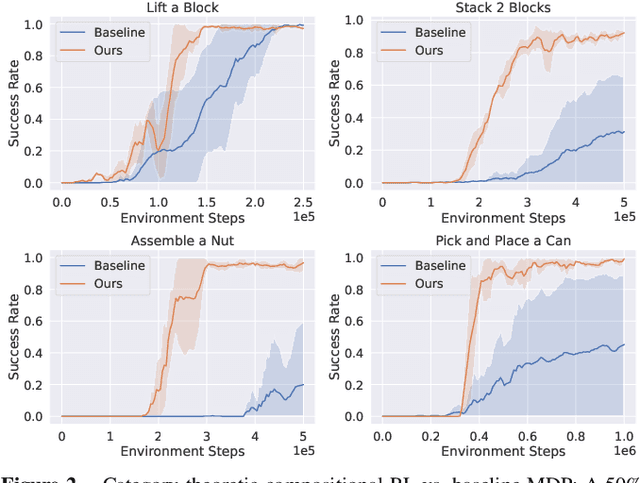
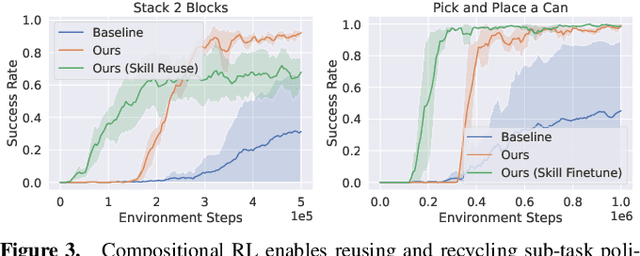
In reinforcement learning, conducting task composition by forming cohesive, executable sequences from multiple tasks remains challenging. However, the ability to (de)compose tasks is a linchpin in developing robotic systems capable of learning complex behaviors. Yet, compositional reinforcement learning is beset with difficulties, including the high dimensionality of the problem space, scarcity of rewards, and absence of system robustness after task composition. To surmount these challenges, we view task composition through the prism of category theory -- a mathematical discipline exploring structures and their compositional relationships. The categorical properties of Markov decision processes untangle complex tasks into manageable sub-tasks, allowing for strategical reduction of dimensionality, facilitating more tractable reward structures, and bolstering system robustness. Experimental results support the categorical theory of reinforcement learning by enabling skill reduction, reuse, and recycling when learning complex robotic arm tasks.

Categorical semantics of compositional reinforcement learning

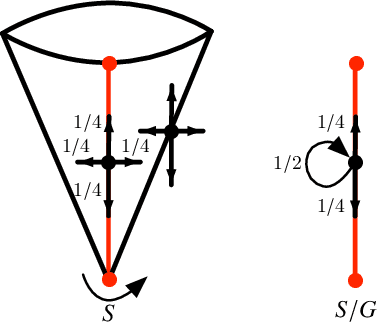
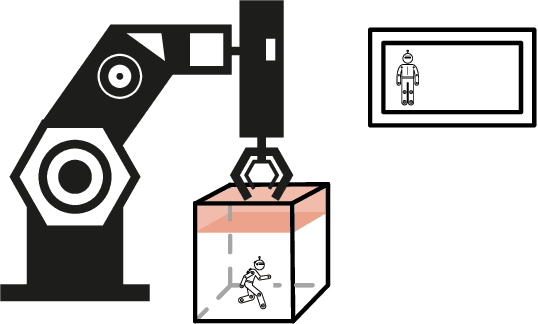
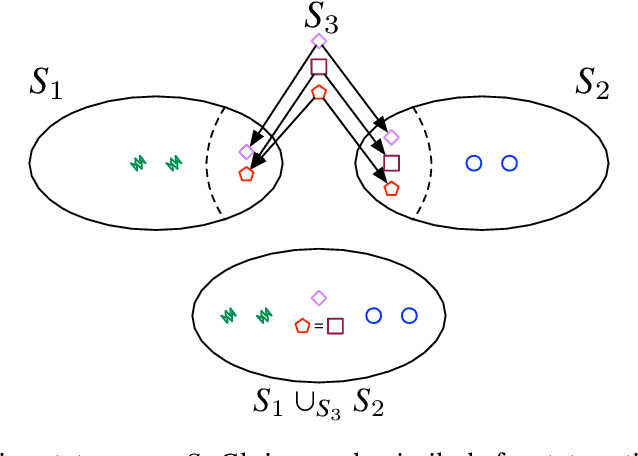
Reinforcement learning (RL) often requires decomposing a problem into subtasks and composing learned behaviors on these tasks. Compositionality in RL has the potential to create modular subtask units that interface with other system capabilities. However, generating compositional models requires the characterization of minimal assumptions for the robustness of the compositional feature. We develop a framework for a \emph{compositional theory} of RL using a categorical point of view. Given the categorical representation of compositionality, we investigate sufficient conditions under which learning-by-parts results in the same optimal policy as learning on the whole. In particular, our approach introduces a category $\mathsf{MDP}$, whose objects are Markov decision processes (MDPs) acting as models of tasks. We show that $\mathsf{MDP}$ admits natural compositional operations, such as certain fiber products and pushouts. These operations make explicit compositional phenomena in RL and unify existing constructions, such as puncturing hazardous states in composite MDPs and incorporating state-action symmetry. We also model sequential task completion by introducing the language of zig-zag diagrams that is an immediate application of the pushout operation in $\mathsf{MDP}$.