Time-Ordered Ad-hoc Resource Sharing for Independent Robotic Agents

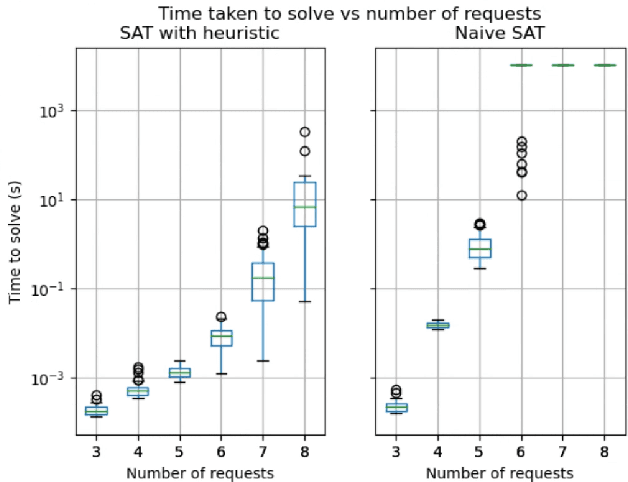
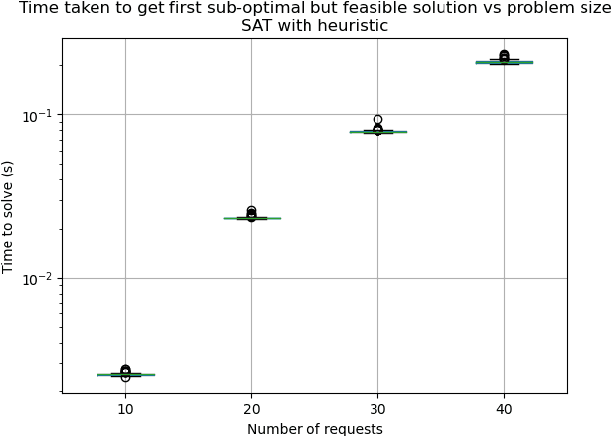
Resource sharing is a crucial part of a multi-robot system. We propose a Boolean satisfiability based approach to resource sharing. Our key contributions are an algorithm for converting any constrained assignment to a weighted-SAT based optimization. We propose a theorem that allows optimal resource assignment problems to be solved via repeated application of a SAT solver. Additionally we show a way to encode continuous time ordering constraints using Conjunctive Normal Form (CNF). We benchmark our new algorithms and show that they can be used in an ad-hoc setting. We test our algorithms on a fleet of simulated and real world robots and show that the algorithms are able to handle real world situations. Our algorithms and test harnesses are opensource and build on Open-RMFs fleet management system.

Footstep and Motion Planning in Semi-unstructured Environments Using Randomized Possibility Graphs

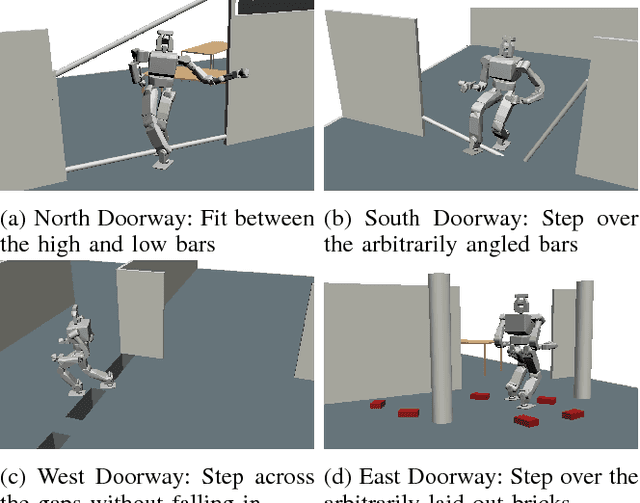
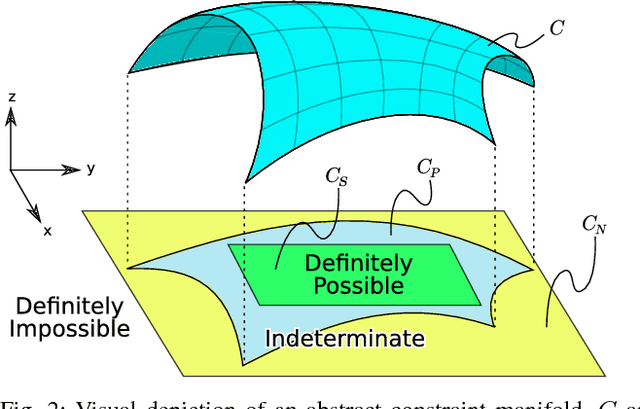
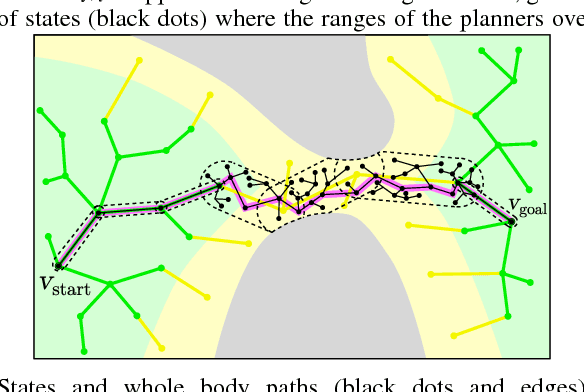
Traversing environments with arbitrary obstacles poses significant challenges for bipedal robots. In some cases, whole body motions may be necessary to maneuver around an obstacle, but most existing footstep planners can only select from a discrete set of predetermined footstep actions; they are unable to utilize the continuum of whole body motion that is truly available to the robot platform. Existing motion planners that can utilize whole body motion tend to struggle with the complexity of large-scale problems. We introduce a planning method, called the "Randomized Possibility Graph", which uses high-level approximations of constraint manifolds to rapidly explore the "possibility" of actions, thereby allowing lower-level motion planners to be utilized more efficiently. We demonstrate simulations of the method working in a variety of semi-unstructured environments. In this context, "semi-unstructured" means the walkable terrain is flat and even, but there are arbitrary 3D obstacles throughout the environment which may need to be stepped over or maneuvered around using whole body motions.

Probabilistic Completeness of Randomized Possibility Graphs Applied to Bipedal Walking in Semi-unstructured Environments

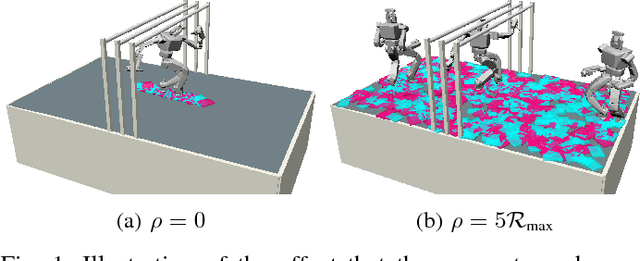
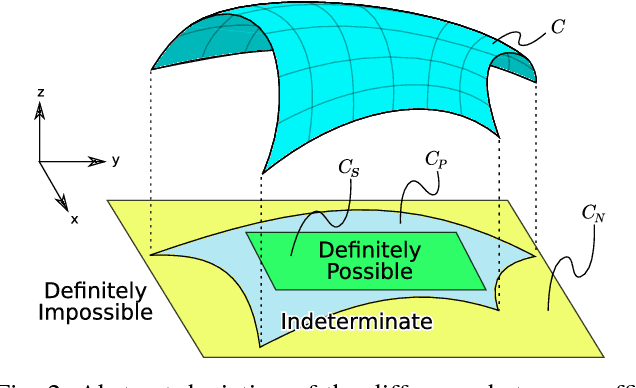
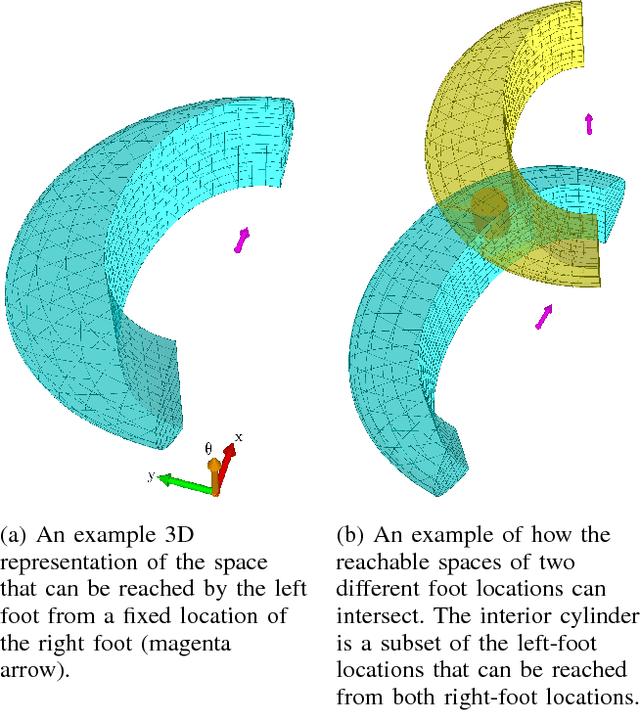
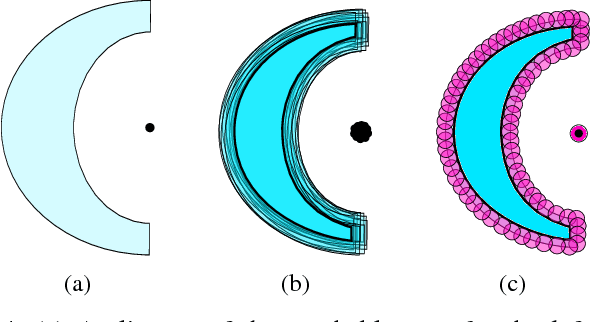
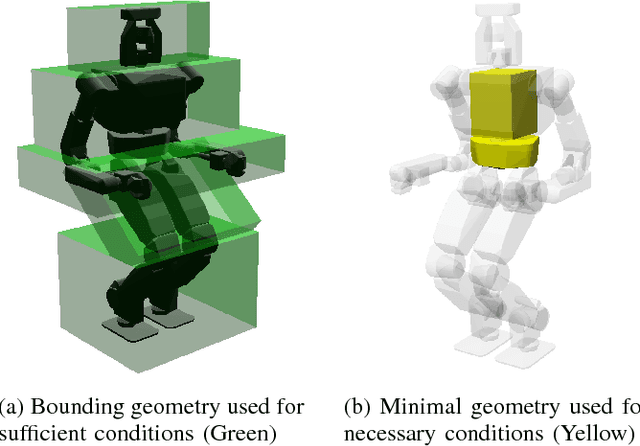
We present a theoretical analysis of a recent whole body motion planning method, the Randomized Possibility Graph, which uses a high-level decomposition of the feasibility constraint manifold in order to rapidly find routes that may lead to a solution. These routes are then examined by lower-level planners to determine feasibility. In this paper, we show that this approach is probabilistically complete for bipedal robots performing quasi-static walking in "semi-unstructured" environments. Furthermore, we show that the decomposition into higher and lower level planners allows for a considerably higher rate of convergence in the probability of finding a solution when one exists. We illustrate this improved convergence with a series of simulated scenarios.

Traversing Environments Using Possibility Graphs with Multiple Action Types

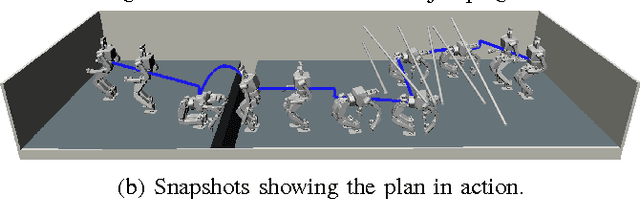
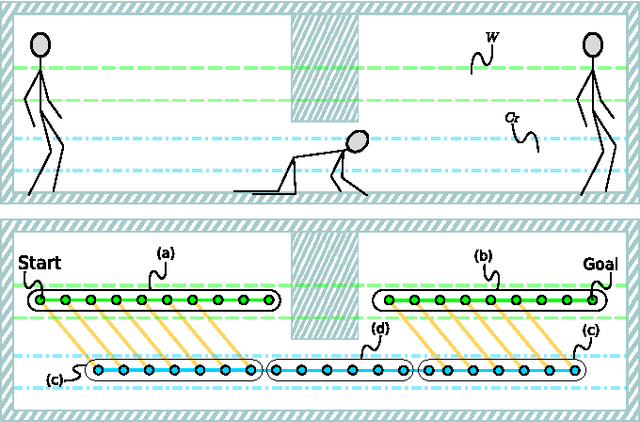
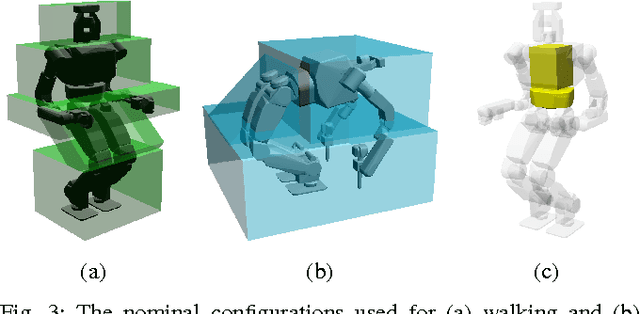
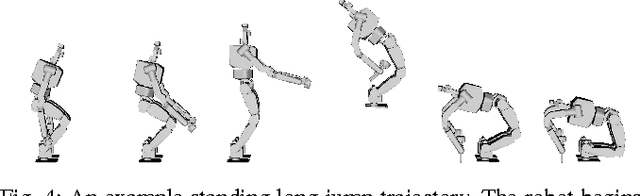
Locomotion for legged robots poses considerable challenges when confronted by obstacles and adverse environments. Footstep planners are typically only designed for one mode of locomotion, but traversing unfavorable environments may require several forms of locomotion to be sequenced together, such as walking, crawling, and jumping. Multi-modal motion planners can be used to address some of these problems, but existing implementations tend to be time-consuming and are limited to quasi-static actions. This paper presents a motion planning method to traverse complex environments using multiple categories of continuous actions. To this end, this paper formulates and exploits the Possibility Graph---which uses high-level approximations of constraint manifolds to rapidly explore the "possibility" of actions---to utilize lower-level single-action motion planners more effectively. We show that the Possibility Graph can quickly find routes through several different challenging environments which require various combinations of actions in order to traverse.

Traversing Environments Using Possibility Graphs for Humanoid Robots

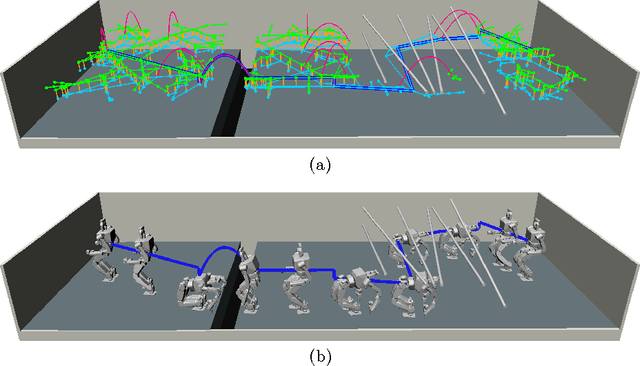
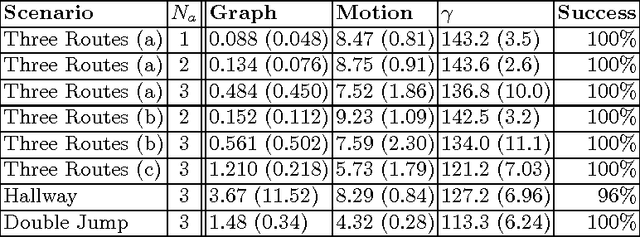
Locomotion for legged robots poses considerable challenges when confronted by obstacles and adverse environments. Footstep planners are typically only designed for one mode of locomotion, but traversing unfavorable environments may require several forms of locomotion to be sequenced together, such as walking, crawling, and jumping. Multi-modal motion planners can be used to address some of these problems, but existing implementations tend to be time-consuming and are limited to quasi-static actions. This paper presents a motion planning method to traverse complex environments using multiple categories of actions. We introduce the concept of the "Possibility Graph", which uses high-level approximations of constraint manifolds to rapidly explore the "possibility" of actions, thereby allowing lower-level single-action motion planners to be utilized more efficiently. We show that the Possibility Graph can quickly find paths through several different challenging environments which require various combinations of actions in order to traverse.