Probabilistic Completeness of Randomized Possibility Graphs Applied to Bipedal Walking in Semi-unstructured Environments
Paper and Code
Feb 01, 2017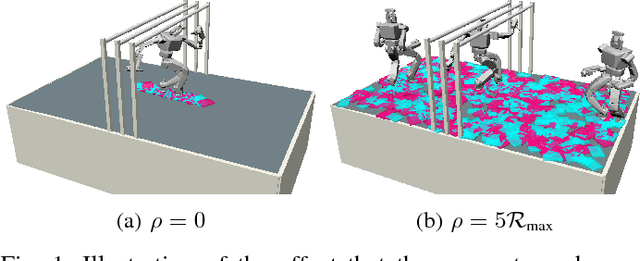
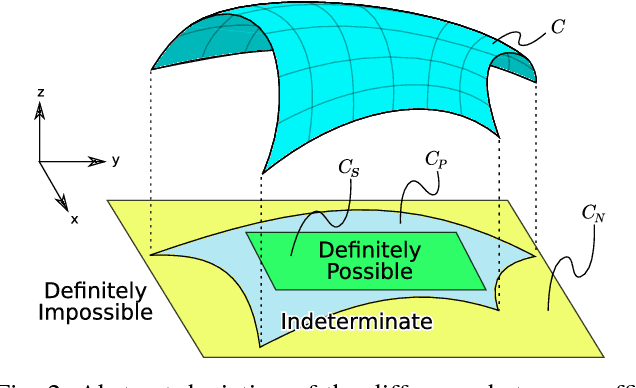
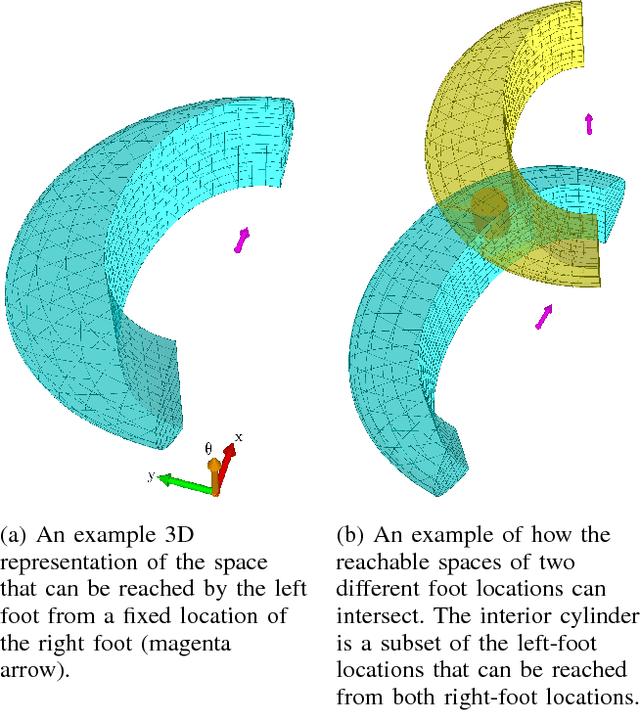
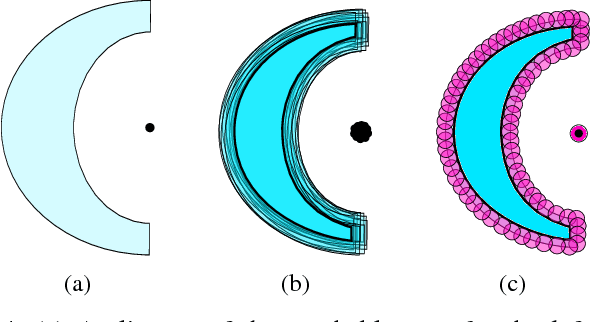
We present a theoretical analysis of a recent whole body motion planning method, the Randomized Possibility Graph, which uses a high-level decomposition of the feasibility constraint manifold in order to rapidly find routes that may lead to a solution. These routes are then examined by lower-level planners to determine feasibility. In this paper, we show that this approach is probabilistically complete for bipedal robots performing quasi-static walking in "semi-unstructured" environments. Furthermore, we show that the decomposition into higher and lower level planners allows for a considerably higher rate of convergence in the probability of finding a solution when one exists. We illustrate this improved convergence with a series of simulated scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge