Multi-Agent Algorithms for Collective Behavior: A structural and application-focused atlas

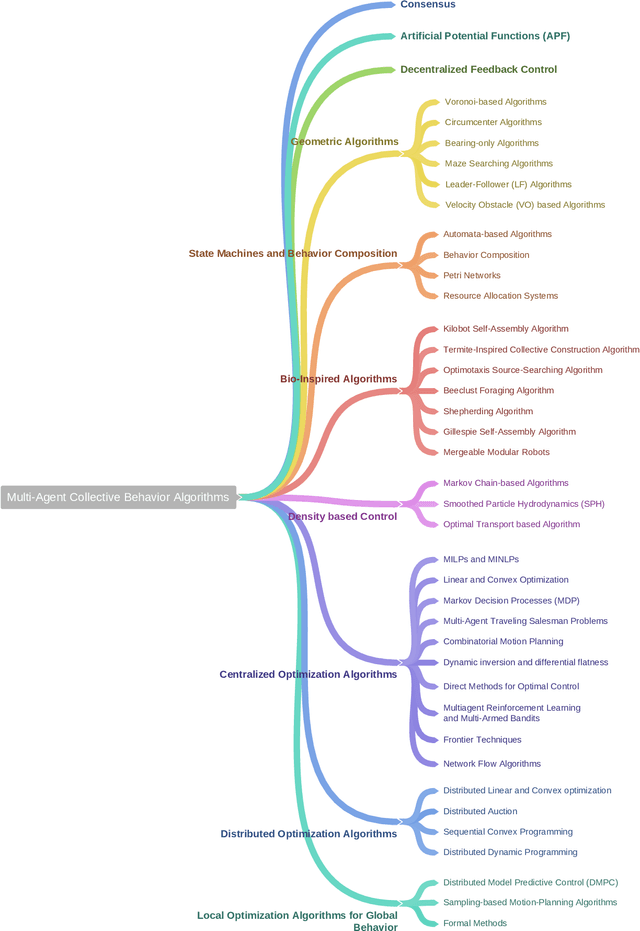
The goal of this paper is to provide a survey and application-focused atlas of collective behavior coordination algorithms for multi-agent systems. We survey the general family of collective behavior algorithms for multi-agent systems and classify them according to their underlying mathematical structure. In doing so, we aim to capture fundamental mathematical properties of algorithms (e.g., scalability with respect to the number of agents and bandwidth use) and to show how the same algorithm or family of algorithms can be used for multiple tasks and applications. Collectively, this paper provides an application-focused atlas of algorithms for collective behavior of multi-agent systems, with three objectives: 1. to act as a tutorial guide to practitioners in the selection of coordination algorithms for a given application; 2. to highlight how mathematically similar algorithms can be used for a variety of tasks, ranging from low-level control to high-level coordination; 3. to explore the state-of-the-art in the field of control of multi-agent systems and identify areas for future research.

Fast Near-Optimal Heterogeneous Task Allocation via Flow Decomposition

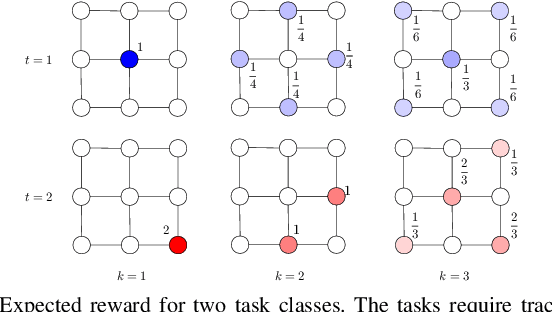
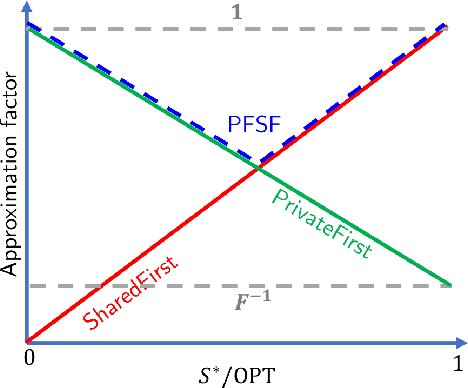
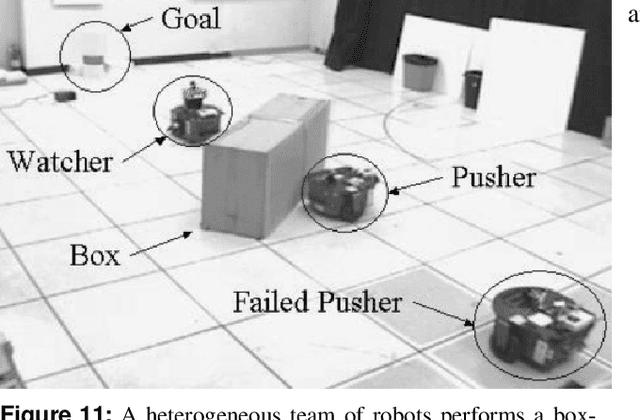
Multi-robot systems are uniquely well-suited to performing complex tasks such as patrolling and tracking, information gathering, and pick-up and delivery problems, offering significantly higher performance than single-robot systems. A fundamental building block in most multi-robot systems is task allocation: assigning robots to tasks (e.g., patrolling an area, or servicing a transportation request) as they appear based on the robots' states to maximize reward. In many practical situations, the allocation must account for heterogeneous capabilities (e.g., availability of appropriate sensors or actuators) to ensure the feasibility of execution, and to promote a higher reward, over a long time horizon. To this end, we present the FlowDec algorithm for efficient heterogeneous task-allocation achieving an approximation factor of at least 1/2 of the optimal reward. Our approach decomposes the heterogeneous problem into several homogeneous subproblems that can be solved efficiently using min-cost flow. Through simulation experiments, we show that our algorithm is faster by several orders of magnitude than a MILP approach.

On Local Computation for Optimization in Multi-Agent Systems

A number of prototypical optimization problems in multi-agent systems (e.g., task allocation and network load-sharing) exhibit a highly local structure: that is, each agent's decision variables are only directly coupled to few other agent's variables through the objective function or the constraints. Nevertheless, existing algorithms for distributed optimization generally do not exploit the locality structure of the problem, requiring all agents to compute or exchange the full set of decision variables. In this paper, we develop a rigorous notion of "locality" that quantifies the degree to which agents can compute their portion of the global solution based solely on information in their local neighborhood. This notion provides a theoretical basis for a rather simple algorithm in which agents individually solve a truncated sub-problem of the global problem, where the size of the sub-problem used depends on the locality of the problem, and the desired accuracy. Numerical results show that the proposed theoretical bounds are remarkably tight for well-conditioned problems.