Uninorm-like parametric activation functions for human-understandable neural models

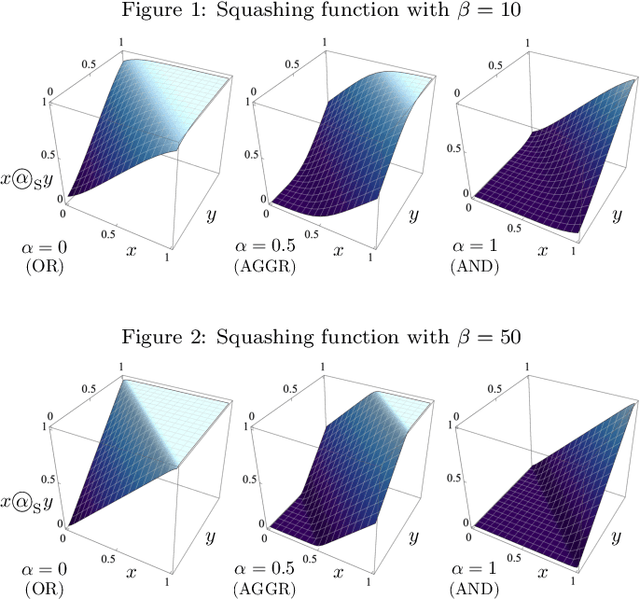
We present a deep learning model for finding human-understandable connections between input features. Our approach uses a parameterized, differentiable activation function, based on the theoretical background of nilpotent fuzzy logic and multi-criteria decision-making (MCDM). The learnable parameter has a semantic meaning indicating the level of compensation between input features. The neural network determines the parameters using gradient descent to find human-understandable relationships between input features. We demonstrate the utility and effectiveness of the model by successfully applying it to classification problems from the UCI Machine Learning Repository.

Leveraging Product as an Activation Function in Deep Networks

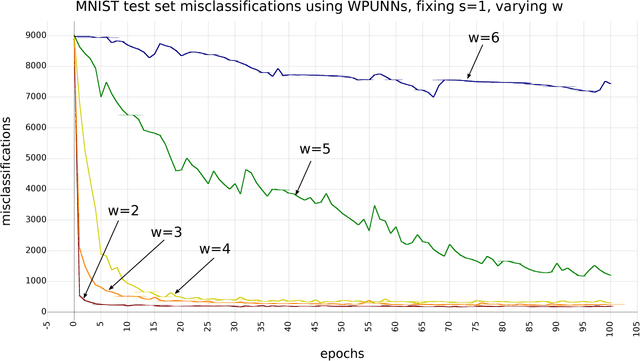
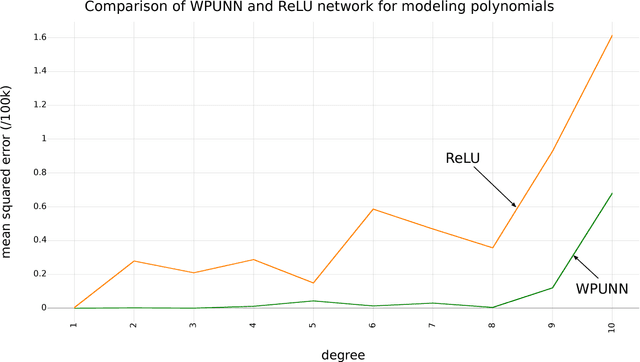
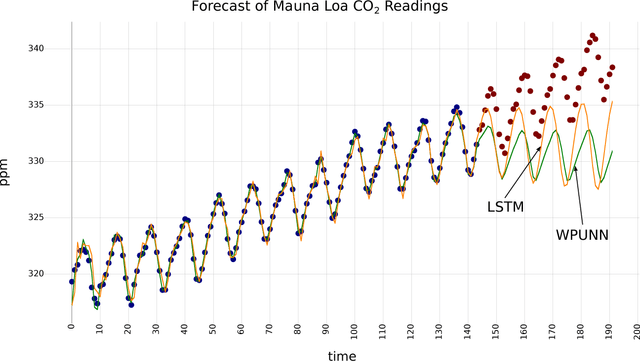
Product unit neural networks (PUNNs) are powerful representational models with a strong theoretical basis, but have proven to be difficult to train with gradient-based optimizers. We present windowed product unit neural networks (WPUNNs), a simple method of leveraging product as a nonlinearity in a neural network. Windowing the product tames the complex gradient surface and enables WPUNNs to learn effectively, solving the problems faced by PUNNs. WPUNNs use product layers between traditional sum layers, capturing the representational power of product units and using the product itself as a nonlinearity. We find the result that this method works as well as traditional nonlinearities like ReLU on the MNIST dataset. We demonstrate that WPUNNs can also generalize gated units in recurrent neural networks, yielding results comparable to LSTM networks.

A parameterized activation function for learning fuzzy logic operations in deep neural networks

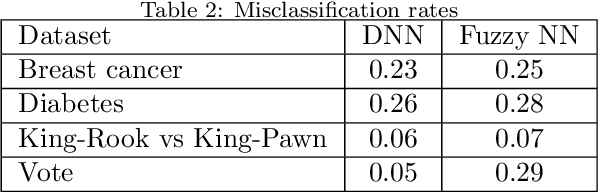
We present a deep learning architecture for learning fuzzy logic expressions. Our model uses an innovative, parameterized, differentiable activation function that can learn a number of logical operations by gradient descent. This activation function allows a neural network to determine the relationships between its input variables and provides insight into the logical significance of learned network parameters. We provide a theoretical basis for this parameterization and demonstrate its effectiveness and utility by successfully applying our model to five classification problems from the UCI Machine Learning Repository.

Deep Learning in Robotics: A Review of Recent Research

Advances in deep learning over the last decade have led to a flurry of research in the application of deep artificial neural networks to robotic systems, with at least thirty papers published on the subject between 2014 and the present. This review discusses the applications, benefits, and limitations of deep learning vis-\`a-vis physical robotic systems, using contemporary research as exemplars. It is intended to communicate recent advances to the wider robotics community and inspire additional interest in and application of deep learning in robotics.

Neural Decomposition of Time-Series Data for Effective Generalization

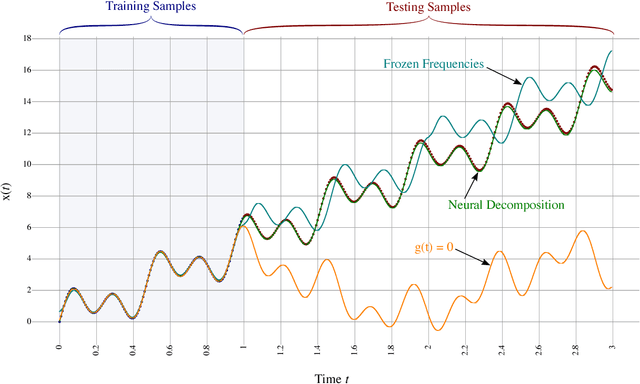
We present a neural network technique for the analysis and extrapolation of time-series data called Neural Decomposition (ND). Units with a sinusoidal activation function are used to perform a Fourier-like decomposition of training samples into a sum of sinusoids, augmented by units with nonperiodic activation functions to capture linear trends and other nonperiodic components. We show how careful weight initialization can be combined with regularization to form a simple model that generalizes well. Our method generalizes effectively on the Mackey-Glass series, a dataset of unemployment rates as reported by the U.S. Department of Labor Statistics, a time-series of monthly international airline passengers, the monthly ozone concentration in downtown Los Angeles, and an unevenly sampled time-series of oxygen isotope measurements from a cave in north India. We find that ND outperforms popular time-series forecasting techniques including LSTM, echo state networks, ARIMA, SARIMA, SVR with a radial basis function, and Gashler and Ashmore's model.

A continuum among logarithmic, linear, and exponential functions, and its potential to improve generalization in neural networks

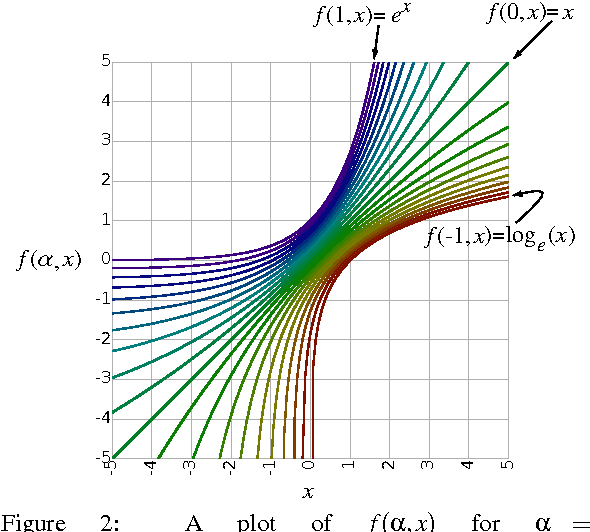
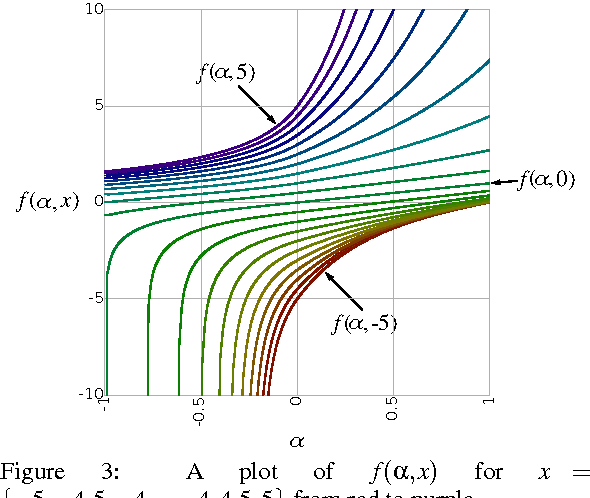
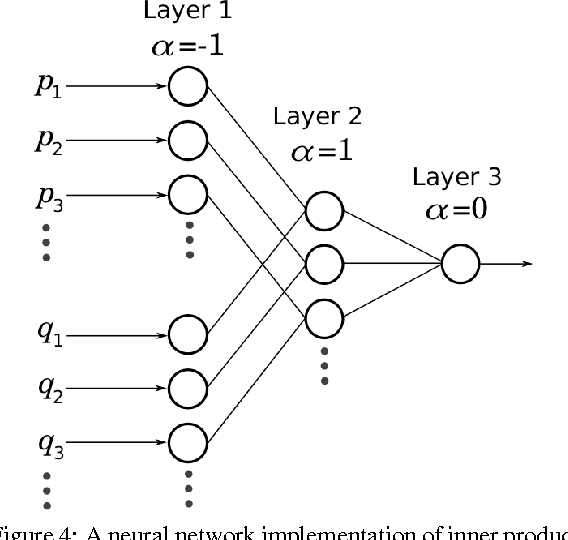
We present the soft exponential activation function for artificial neural networks that continuously interpolates between logarithmic, linear, and exponential functions. This activation function is simple, differentiable, and parameterized so that it can be trained as the rest of the network is trained. We hypothesize that soft exponential has the potential to improve neural network learning, as it can exactly calculate many natural operations that typical neural networks can only approximate, including addition, multiplication, inner product, distance, polynomials, and sinusoids.

A Minimal Architecture for General Cognition

A minimalistic cognitive architecture called MANIC is presented. The MANIC architecture requires only three function approximating models, and one state machine. Even with so few major components, it is theoretically sufficient to achieve functional equivalence with all other cognitive architectures, and can be practically trained. Instead of seeking to transfer architectural inspiration from biology into artificial intelligence, MANIC seeks to minimize novelty and follow the most well-established constructs that have evolved within various sub-fields of data science. From this perspective, MANIC offers an alternate approach to a long-standing objective of artificial intelligence. This paper provides a theoretical analysis of the MANIC architecture.

Training Deep Fourier Neural Networks To Fit Time-Series Data

We present a method for training a deep neural network containing sinusoidal activation functions to fit to time-series data. Weights are initialized using a fast Fourier transform, then trained with regularization to improve generalization. A simple dynamic parameter tuning method is employed to adjust both the learning rate and regularization term, such that stability and efficient training are both achieved. We show how deeper layers can be utilized to model the observed sequence using a sparser set of sinusoid units, and how non-uniform regularization can improve generalization by promoting the shifting of weight toward simpler units. The method is demonstrated with time-series problems to show that it leads to effective extrapolation of nonlinear trends.

Missing Value Imputation With Unsupervised Backpropagation

Many data mining and data analysis techniques operate on dense matrices or complete tables of data. Real-world data sets, however, often contain unknown values. Even many classification algorithms that are designed to operate with missing values still exhibit deteriorated accuracy. One approach to handling missing values is to fill in (impute) the missing values. In this paper, we present a technique for unsupervised learning called Unsupervised Backpropagation (UBP), which trains a multi-layer perceptron to fit to the manifold sampled by a set of observed point-vectors. We evaluate UBP with the task of imputing missing values in datasets, and show that UBP is able to predict missing values with significantly lower sum-squared error than other collaborative filtering and imputation techniques. We also demonstrate with 24 datasets and 9 supervised learning algorithms that classification accuracy is usually higher when randomly-withheld values are imputed using UBP, rather than with other methods.