Fairness Testing through Extreme Value Theory

Data-driven software is increasingly being used as a critical component of automated decision-support systems. Since this class of software learns its logic from historical data, it can encode or amplify discriminatory practices. Previous research on algorithmic fairness has focused on improving average-case fairness. On the other hand, fairness at the extreme ends of the spectrum, which often signifies lasting and impactful shifts in societal attitudes, has received significantly less emphasis. Leveraging the statistics of extreme value theory (EVT), we propose a novel fairness criterion called extreme counterfactual discrimination (ECD). This criterion estimates the worst-case amounts of disadvantage in outcomes for individuals solely based on their memberships in a protected group. Utilizing tools from search-based software engineering and generative AI, we present a randomized algorithm that samples a statistically significant set of points from the tail of ML outcome distributions even if the input dataset lacks a sufficient number of relevant samples. We conducted several experiments on four ML models (deep neural networks, logistic regression, and random forests) over 10 socially relevant tasks from the literature on algorithmic fairness. First, we evaluate the generative AI methods and find that they generate sufficient samples to infer valid EVT distribution in 95% of cases. Remarkably, we found that the prevalent bias mitigators reduce the average-case discrimination but increase the worst-case discrimination significantly in 5% of cases. We also observed that even the tail-aware mitigation algorithm -- MiniMax-Fairness -- increased the worst-case discrimination in 30% of cases. We propose a novel ECD-based mitigator that improves fairness in the tail in 90% of cases with no degradation of the average-case discrimination.

Predicting Fairness of ML Software Configuration

This paper investigates the relationships between hyperparameters of machine learning and fairness. Data-driven solutions are increasingly used in critical socio-technical applications where ensuring fairness is important. Rather than explicitly encoding decision logic via control and data structures, the ML developers provide input data, perform some pre-processing, choose ML algorithms, and tune hyperparameters (HPs) to infer a program that encodes the decision logic. Prior works report that the selection of HPs can significantly influence fairness. However, tuning HPs to find an ideal trade-off between accuracy, precision, and fairness has remained an expensive and tedious task. Can we predict fairness of HP configuration for a given dataset? Are the predictions robust to distribution shifts? We focus on group fairness notions and investigate the HP space of 5 training algorithms. We first find that tree regressors and XGBoots significantly outperformed deep neural networks and support vector machines in accurately predicting the fairness of HPs. When predicting the fairness of ML hyperparameters under temporal distribution shift, the tree regressors outperforms the other algorithms with reasonable accuracy. However, the precision depends on the ML training algorithm, dataset, and protected attributes. For example, the tree regressor model was robust for training data shift from 2014 to 2018 on logistic regression and discriminant analysis HPs with sex as the protected attribute; but not for race and other training algorithms. Our method provides a sound framework to efficiently perform fine-tuning of ML training algorithms and understand the relationships between HPs and fairness.

An AlphaZero-Inspired Approach to Solving Search Problems

AlphaZero and its extension MuZero are computer programs that use machine-learning techniques to play at a superhuman level in chess, go, and a few other games. They achieved this level of play solely with reinforcement learning from self-play, without any domain knowledge except the game rules. It is a natural idea to adapt the methods and techniques used in AlphaZero for solving search problems such as the Boolean satisfiability problem (in its search version). Given a search problem, how to represent it for an AlphaZero-inspired solver? What are the "rules of solving" for this search problem? We describe possible representations in terms of easy-instance solvers and self-reductions, and we give examples of such representations for the satisfiability problem. We also describe a version of Monte Carlo tree search adapted for search problems.

Uninorm-like parametric activation functions for human-understandable neural models

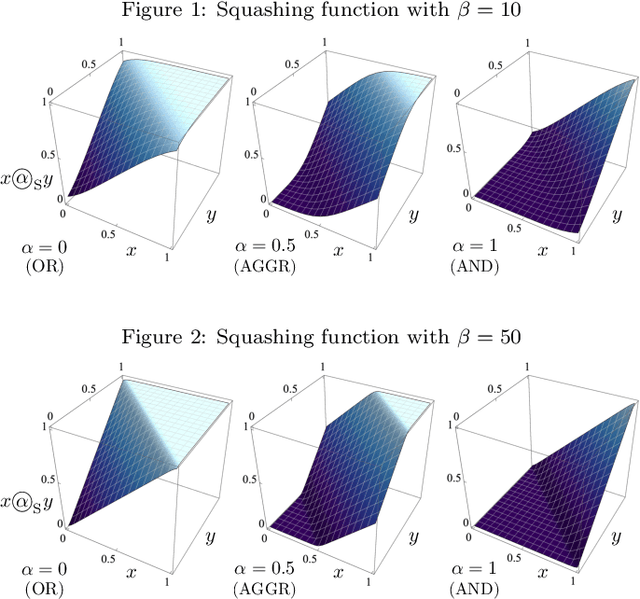
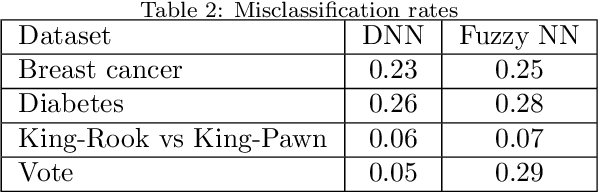
We present a deep learning model for finding human-understandable connections between input features. Our approach uses a parameterized, differentiable activation function, based on the theoretical background of nilpotent fuzzy logic and multi-criteria decision-making (MCDM). The learnable parameter has a semantic meaning indicating the level of compensation between input features. The neural network determines the parameters using gradient descent to find human-understandable relationships between input features. We demonstrate the utility and effectiveness of the model by successfully applying it to classification problems from the UCI Machine Learning Repository.