Leveraging Product as an Activation Function in Deep Networks

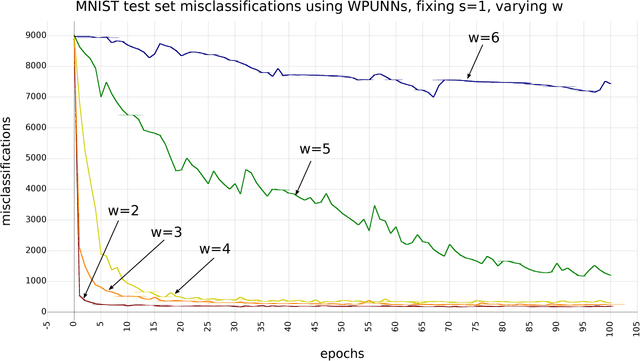
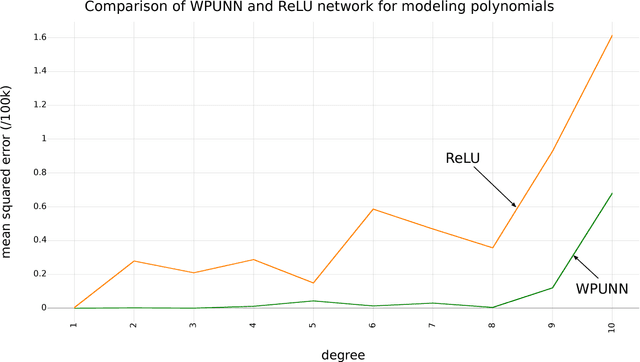
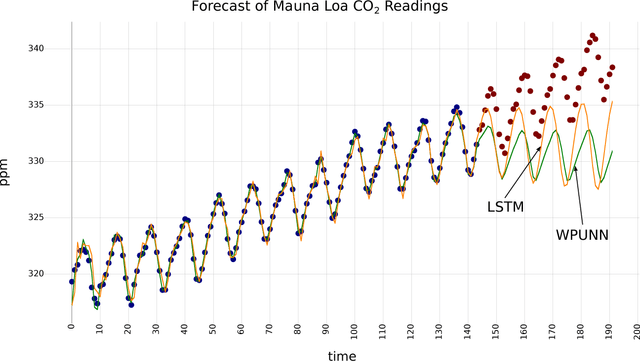
Product unit neural networks (PUNNs) are powerful representational models with a strong theoretical basis, but have proven to be difficult to train with gradient-based optimizers. We present windowed product unit neural networks (WPUNNs), a simple method of leveraging product as a nonlinearity in a neural network. Windowing the product tames the complex gradient surface and enables WPUNNs to learn effectively, solving the problems faced by PUNNs. WPUNNs use product layers between traditional sum layers, capturing the representational power of product units and using the product itself as a nonlinearity. We find the result that this method works as well as traditional nonlinearities like ReLU on the MNIST dataset. We demonstrate that WPUNNs can also generalize gated units in recurrent neural networks, yielding results comparable to LSTM networks.

A parameterized activation function for learning fuzzy logic operations in deep neural networks

We present a deep learning architecture for learning fuzzy logic expressions. Our model uses an innovative, parameterized, differentiable activation function that can learn a number of logical operations by gradient descent. This activation function allows a neural network to determine the relationships between its input variables and provides insight into the logical significance of learned network parameters. We provide a theoretical basis for this parameterization and demonstrate its effectiveness and utility by successfully applying our model to five classification problems from the UCI Machine Learning Repository.

Neural Decomposition of Time-Series Data for Effective Generalization

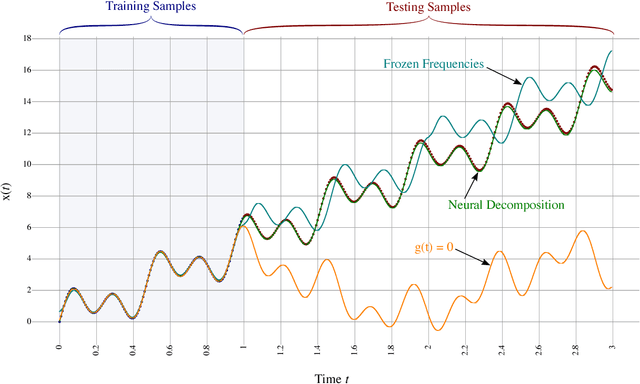
We present a neural network technique for the analysis and extrapolation of time-series data called Neural Decomposition (ND). Units with a sinusoidal activation function are used to perform a Fourier-like decomposition of training samples into a sum of sinusoids, augmented by units with nonperiodic activation functions to capture linear trends and other nonperiodic components. We show how careful weight initialization can be combined with regularization to form a simple model that generalizes well. Our method generalizes effectively on the Mackey-Glass series, a dataset of unemployment rates as reported by the U.S. Department of Labor Statistics, a time-series of monthly international airline passengers, the monthly ozone concentration in downtown Los Angeles, and an unevenly sampled time-series of oxygen isotope measurements from a cave in north India. We find that ND outperforms popular time-series forecasting techniques including LSTM, echo state networks, ARIMA, SARIMA, SVR with a radial basis function, and Gashler and Ashmore's model.

A continuum among logarithmic, linear, and exponential functions, and its potential to improve generalization in neural networks

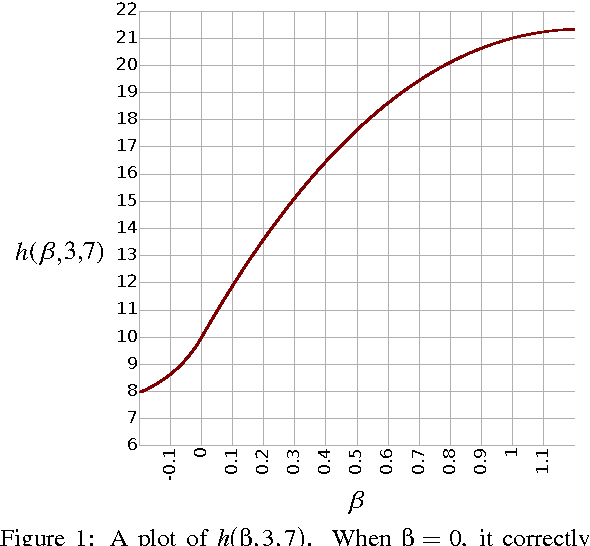
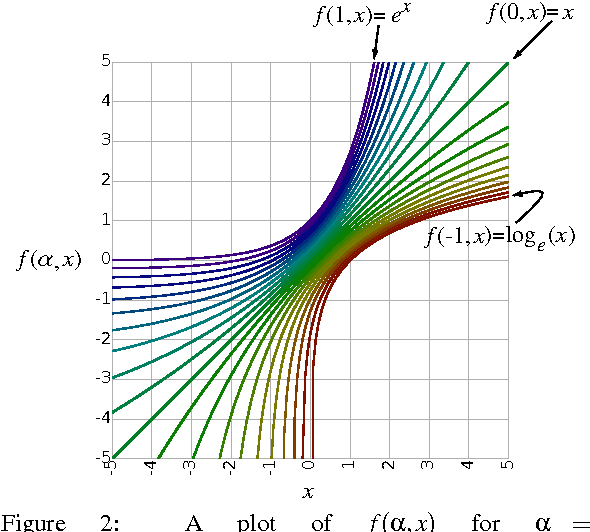
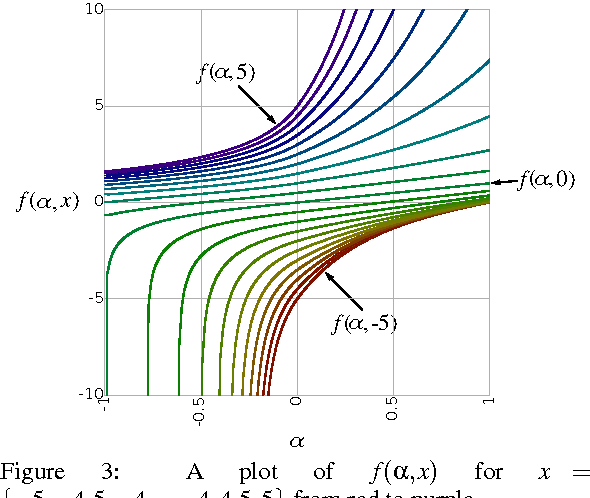
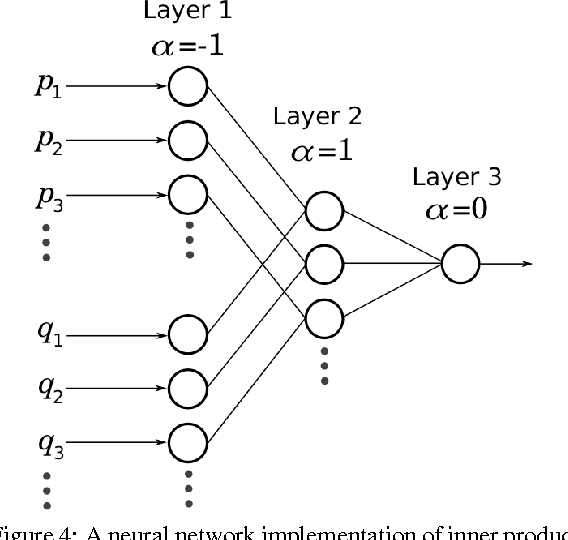
We present the soft exponential activation function for artificial neural networks that continuously interpolates between logarithmic, linear, and exponential functions. This activation function is simple, differentiable, and parameterized so that it can be trained as the rest of the network is trained. We hypothesize that soft exponential has the potential to improve neural network learning, as it can exactly calculate many natural operations that typical neural networks can only approximate, including addition, multiplication, inner product, distance, polynomials, and sinusoids.