A continuum among logarithmic, linear, and exponential functions, and its potential to improve generalization in neural networks
Paper and Code
Feb 03, 2016
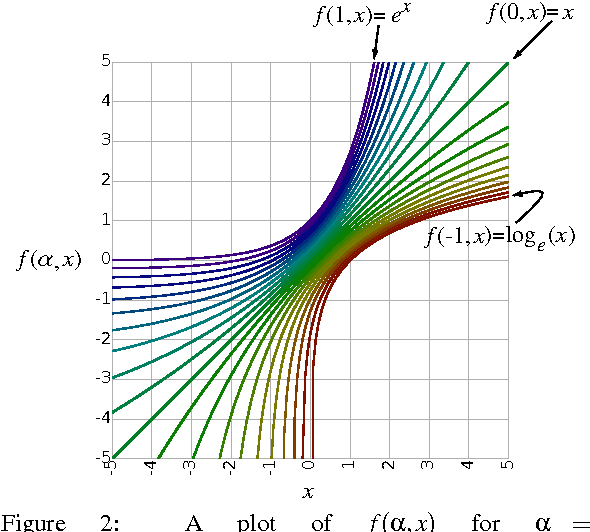
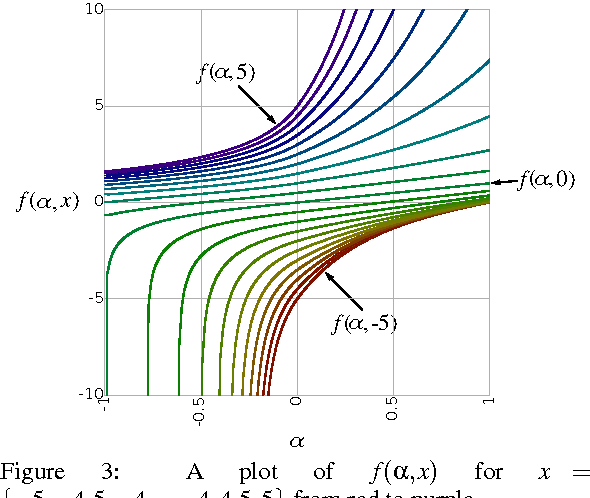
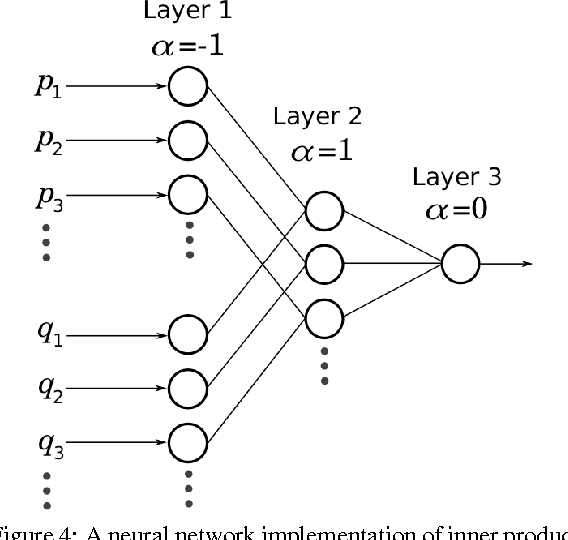
We present the soft exponential activation function for artificial neural networks that continuously interpolates between logarithmic, linear, and exponential functions. This activation function is simple, differentiable, and parameterized so that it can be trained as the rest of the network is trained. We hypothesize that soft exponential has the potential to improve neural network learning, as it can exactly calculate many natural operations that typical neural networks can only approximate, including addition, multiplication, inner product, distance, polynomials, and sinusoids.
* 6 pages, 8 figures, conference, In Proceedings of Knowledge Discovery
and Information Retrieval (KDIR) 2015, Lisbon, Portugal, December 2015
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge