Minimax Robust Landmine Detection Using Forward-Looking Ground-Penetrating Radar

We propose a robust likelihood-ratio test (LRT) to detect landmines and unexploded ordnance using a forward-looking ground-penetrating radar. Instead of modeling the distributions of the target and clutter returns with parametric families, we construct a band of feasible probability densities under each hypothesis. The LRT is then devised based on the least favorable densities within the bands. This detector is designed to maximize the worst-case performance over all feasible density pairs and, hence, does not require strong assumptions about the clutter and noise distributions. The proposed technique is evaluated using electromagnetic field simulation data of shallow-buried targets. We show that, compared to detectors based on parametric models, robust detectors can lead to significantly reduced false alarm rates, particularly in cases where there is a mismatch between the assumed model and the true distributions.

Asymptotically Optimal Procedures for Sequential Joint Detection and Estimation

We investigate the problem of jointly testing multiple hypotheses and estimating a random parameter of the underlying distribution in a sequential setup. The aim is to jointly infer the true hypothesis and the true parameter while using on average as few samples as possible and keeping the detection and estimation errors below predefined levels. Based on mild assumptions on the underlying model, we propose an asymptotically optimal procedure, i.e., a procedure that becomes optimal when the tolerated detection and estimation error levels tend to zero. The implementation of the resulting asymptotically optimal stopping rule is computationally cheap and, hence, applicable for high-dimensional data. We further propose a projected quasi-Newton method to optimally chose the coefficients that parameterize the instantaneous cost function such that the constraints are fulfilled with equality. The proposed theory is validated by numerical examples.

Nonparametric Estimation of the Fisher Information and Its Applications

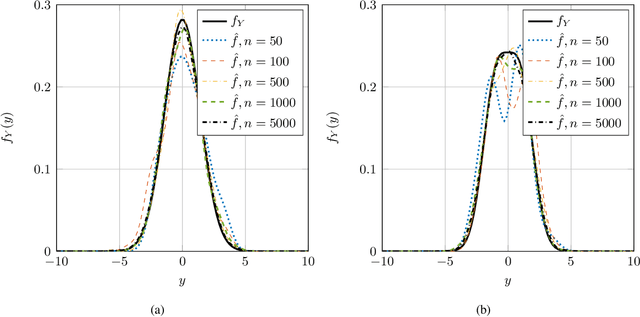
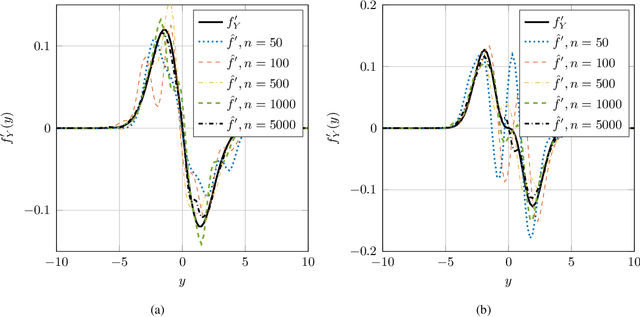
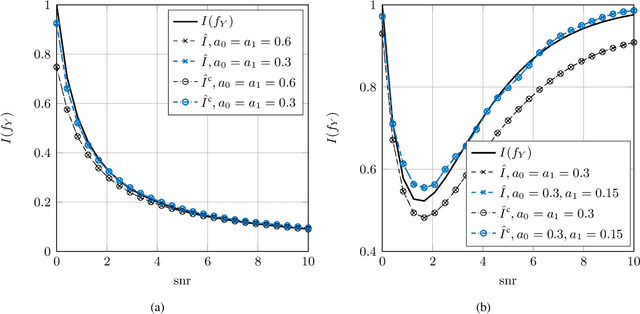
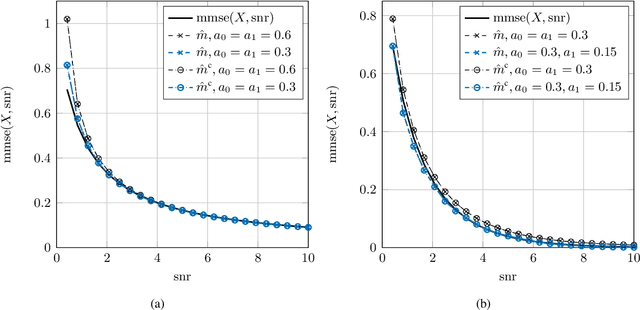
This paper considers the problem of estimation of the Fisher information for location from a random sample of size $n$. First, an estimator proposed by Bhattacharya is revisited and improved convergence rates are derived. Second, a new estimator, termed a clipped estimator, is proposed. Superior upper bounds on the rates of convergence can be shown for the new estimator compared to the Bhattacharya estimator, albeit with different regularity conditions. Third, both of the estimators are evaluated for the practically relevant case of a random variable contaminated by Gaussian noise. Moreover, using Brown's identity, which relates the Fisher information and the minimum mean squared error (MMSE) in Gaussian noise, two corresponding consistent estimators for the MMSE are proposed. Simulation examples for the Bhattacharya estimator and the clipped estimator as well as the MMSE estimators are presented. The examples demonstrate that the clipped estimator can significantly reduce the required sample size to guarantee a specific confidence interval compared to the Bhattacharya estimator.