Causal Influence in Federated Edge Inference

In this paper, we consider a setting where heterogeneous agents with connectivity are performing inference using unlabeled streaming data. Observed data are only partially informative about the target variable of interest. In order to overcome the uncertainty, agents cooperate with each other by exchanging their local inferences with and through a fusion center. To evaluate how each agent influences the overall decision, we adopt a causal framework in order to distinguish the actual influence of agents from mere correlations within the decision-making process. Various scenarios reflecting different agent participation patterns and fusion center policies are investigated. We derive expressions to quantify the causal impact of each agent on the joint decision, which could be beneficial for anticipating and addressing atypical scenarios, such as adversarial attacks or system malfunctions. We validate our theoretical results with numerical simulations and a real-world application of multi-camera crowd counting.

Detection of Malicious Agents in Social Learning

Social learning is a non-Bayesian framework for distributed hypothesis testing aimed at learning the true state of the environment. Traditionally, the agents are assumed to receive observations conditioned on the same true state, although it is also possible to examine the case of heterogeneous models across the graph. One important special case is when heterogeneity is caused by the presence of malicious agents whose goal is to move the agents towards a wrong hypothesis. In this work, we propose an algorithm that allows to discover the true state of every individual agent based on the sequence of their beliefs. In so doing, the methodology is also able to locate malicious behavior.

Social Learning in Community Structured Graphs

Traditional social learning frameworks consider environments with a homogeneous state, where each agent receives observations conditioned on that true state of nature. In this work, we relax this assumption and study the distributed hypothesis testing problem in a heterogeneous environment, where each agent can receive observations conditioned on their own personalized state of nature (or truth). This situation arises in many scenarios, such as when sensors are spatially distributed, or when individuals in a social network have differing views or opinions. In these heterogeneous contexts, the graph topology admits a block structure. We study social learning under personalized (or multitask) models and examine their convergence behavior.

Causal Influences over Social Learning Networks

This paper investigates causal influences between agents linked by a social graph and interacting over time. In particular, the work examines the dynamics of social learning models and distributed decision-making protocols, and derives expressions that reveal the causal relations between pairs of agents and explain the flow of influence over the network. The results turn out to be dependent on the graph topology and the level of information that each agent has about the inference problem they are trying to solve. Using these conclusions, the paper proposes an algorithm to rank the overall influence between agents to discover highly influential agents. It also provides a method to learn the necessary model parameters from raw observational data. The results and the proposed algorithm are illustrated by considering both synthetic data and real Twitter data.

Non-Asymptotic Performance of Social Machine Learning Under Limited Data

This paper studies the probability of error associated with the social machine learning framework, which involves an independent training phase followed by a cooperative decision-making phase over a graph. This framework addresses the problem of classifying a stream of unlabeled data in a distributed manner. We consider two kinds of classification tasks with limited observations in the prediction phase, namely, the statistical classification task and the single-sample classification task. For each task, we describe the distributed learning rule and analyze the probability of error accordingly. To do so, we first introduce a stronger consistent training condition that involves the margin distributions generated by the trained classifiers. Based on this condition, we derive an upper bound on the probability of error for both tasks, which depends on the statistical properties of the data and the combination policy used to combine the distributed classifiers. For the statistical classification problem, we employ the geometric social learning rule and conduct a non-asymptotic performance analysis. An exponential decay of the probability of error with respect to the number of unlabeled samples is observed in the upper bound. For the single-sample classification task, a distributed learning rule that functions as an ensemble classifier is constructed. An upper bound on the probability of error of this ensemble classifier is established.

On the Fusion Strategies for Federated Decision Making

We consider the problem of information aggregation in federated decision making, where a group of agents collaborate to infer the underlying state of nature without sharing their private data with the central processor or each other. We analyze the non-Bayesian social learning strategy in which agents incorporate their individual observations into their opinions (i.e., soft-decisions) with Bayes rule, and the central processor aggregates these opinions by arithmetic or geometric averaging. Building on our previous work, we establish that both pooling strategies result in asymptotic normality characterization of the system, which, for instance, can be utilized in order to give approximate expressions for the error probability. We verify the theoretical findings with simulations and compare both strategies.

Policy Evaluation in Decentralized POMDPs with Belief Sharing

Most works on multi-agent reinforcement learning focus on scenarios where the state of the environment is fully observable. In this work, we consider a cooperative policy evaluation task in which agents are not assumed to observe the environment state directly. Instead, agents can only have access to noisy observations and to belief vectors. It is well-known that finding global posterior distributions under multi-agent settings is generally NP-hard. As a remedy, we propose a fully decentralized belief forming strategy that relies on individual updates and on localized interactions over a communication network. In addition to the exchange of the beliefs, agents exploit the communication network by exchanging value function parameter estimates as well. We analytically show that the proposed strategy allows information to diffuse over the network, which in turn allows the agents' parameters to have a bounded difference with a centralized baseline. A multi-sensor target tracking application is considered in the simulations.

Distributed Bayesian Learning of Dynamic States

This work studies networked agents cooperating to track a dynamical state of nature under partial information. The proposed algorithm is a distributed Bayesian filtering algorithm for finite-state hidden Markov models (HMMs). It can be used for sequential state estimation tasks, as well as for modeling opinion formation over social networks under dynamic environments. We show that the disagreement with the optimal centralized solution is asymptotically bounded for the class of geometrically ergodic state transition models, which includes rapidly changing models. We also derive recursions for calculating the probability of error and establish convergence under Gaussian observation models. Simulations are provided to illustrate the theory and to compare against alternative approaches.

Discovering Influencers in Opinion Formation over Social Graphs

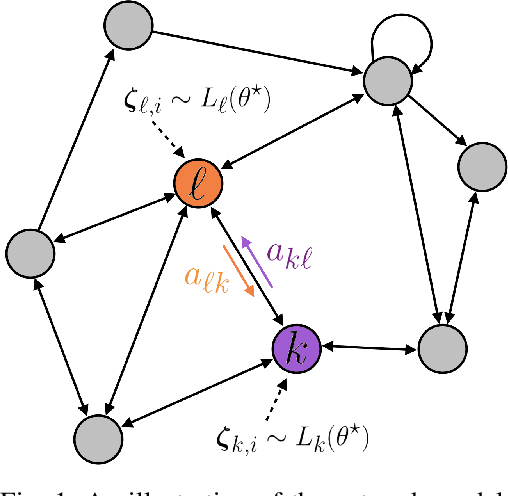
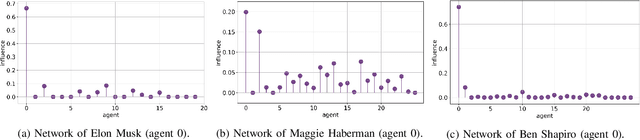
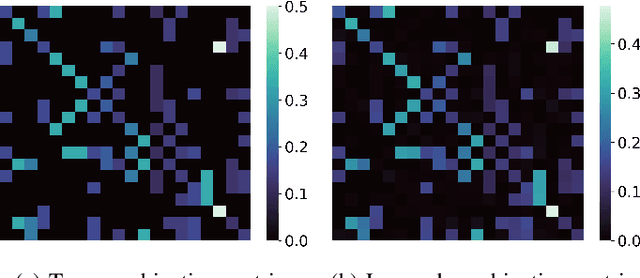
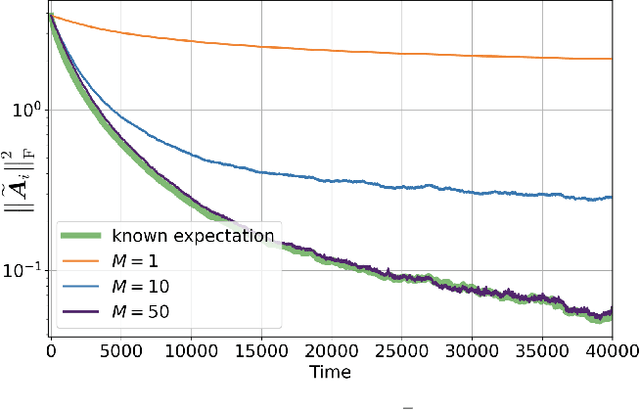
The adaptive social learning paradigm helps model how networked agents are able to form opinions on a state of nature and track its drifts in a changing environment. In this framework, the agents repeatedly update their beliefs based on private observations and exchange the beliefs with their neighbors. In this work, it is shown how the sequence of publicly exchanged beliefs over time allows users to discover rich information about the underlying network topology and about the flow of information over graph. In particular, it is shown that it is possible (i) to identify the influence of each individual agent to the objective of truth learning, (ii) to discover how well informed each agent is, (iii) to quantify the pairwise influences between agents, and (iv) to learn the underlying network topology. The algorithm derived herein is also able to work under non-stationary environments where either the true state of nature or the network topology are allowed to drift over time. We apply the proposed algorithm to different subnetworks of Twitter users, and identify the most influential and central agents merely by using their public tweets (posts).

A Fundamental Limit of Distributed Hypothesis Testing Under Memoryless Quantization

We study a distributed hypothesis testing setup where peripheral nodes send quantized data to the fusion center in a memoryless fashion. The \emph{expected} number of bits sent by each node under the null hypothesis is kept limited. We characterize the optimal decay rate of the mis-detection (type-II error) probability provided that false alarms (type-I error) are rare, and study the tradeoff between the communication rate and maximal type-II error decay rate. We resort to rate-distortion methods to provide upper bounds to the tradeoff curve and show that at high rates lattice quantization achieves near-optimal performance. We also characterize the tradeoff for the case where nodes are allowed to record and quantize a fixed number of samples. Moreover, under sum-rate constraints, we show that an upper bound to the tradeoff curve is obtained with a water-filling solution.