Emre Telatar
On the Fusion Strategies for Federated Decision Making
Mar 10, 2023
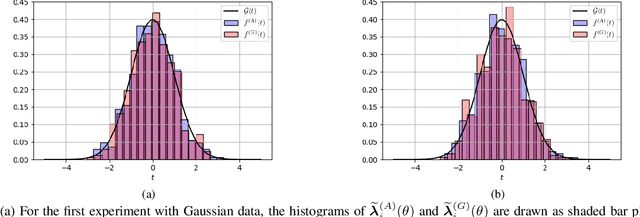
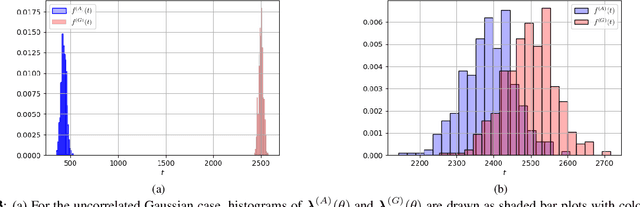
Abstract:We consider the problem of information aggregation in federated decision making, where a group of agents collaborate to infer the underlying state of nature without sharing their private data with the central processor or each other. We analyze the non-Bayesian social learning strategy in which agents incorporate their individual observations into their opinions (i.e., soft-decisions) with Bayes rule, and the central processor aggregates these opinions by arithmetic or geometric averaging. Building on our previous work, we establish that both pooling strategies result in asymptotic normality characterization of the system, which, for instance, can be utilized in order to give approximate expressions for the error probability. We verify the theoretical findings with simulations and compare both strategies.
A Fundamental Limit of Distributed Hypothesis Testing Under Memoryless Quantization
Jun 24, 2022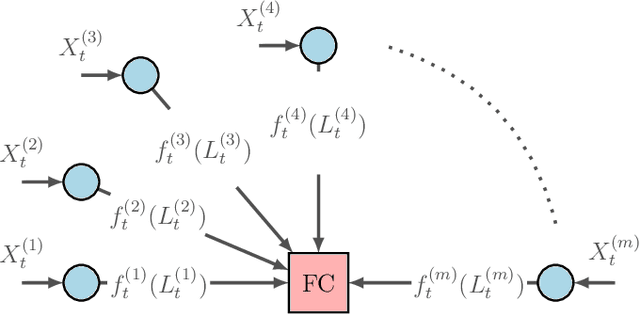
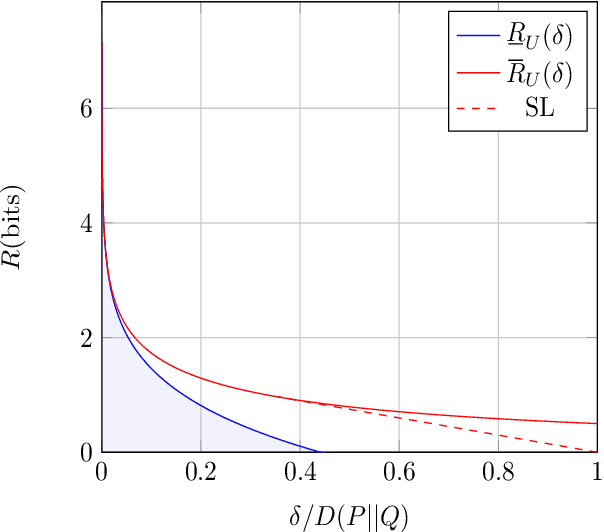

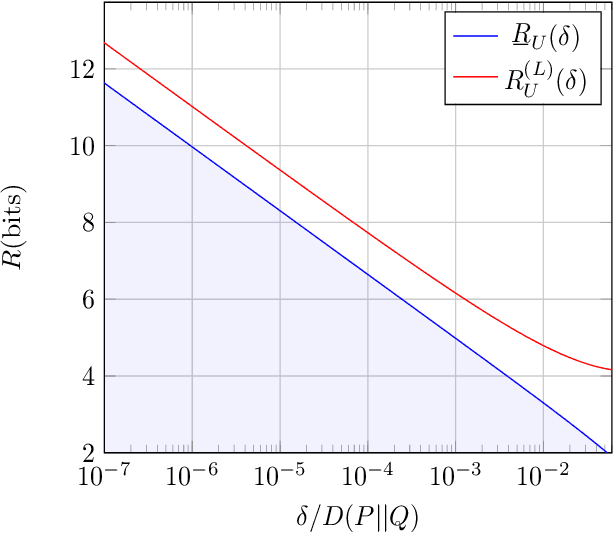
Abstract:We study a distributed hypothesis testing setup where peripheral nodes send quantized data to the fusion center in a memoryless fashion. The \emph{expected} number of bits sent by each node under the null hypothesis is kept limited. We characterize the optimal decay rate of the mis-detection (type-II error) probability provided that false alarms (type-I error) are rare, and study the tradeoff between the communication rate and maximal type-II error decay rate. We resort to rate-distortion methods to provide upper bounds to the tradeoff curve and show that at high rates lattice quantization achieves near-optimal performance. We also characterize the tradeoff for the case where nodes are allowed to record and quantize a fixed number of samples. Moreover, under sum-rate constraints, we show that an upper bound to the tradeoff curve is obtained with a water-filling solution.
On the Arithmetic and Geometric Fusion of Beliefs for Distributed Inference
Apr 28, 2022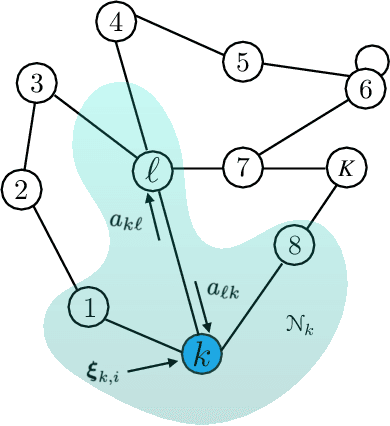
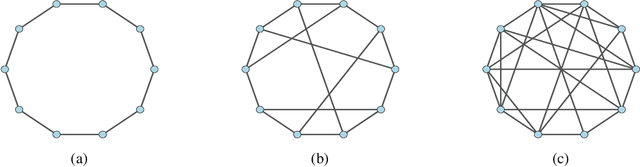
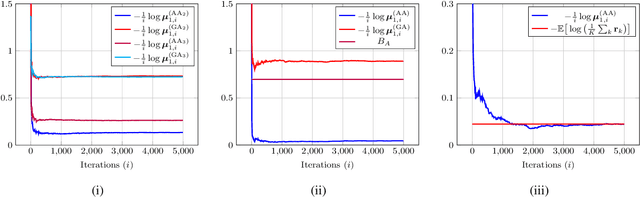
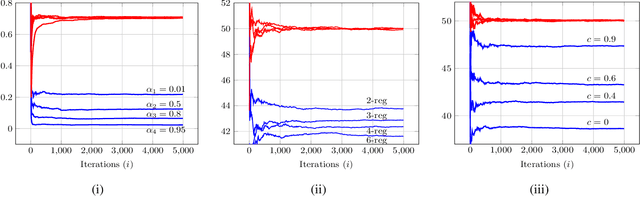
Abstract:We study the asymptotic learning rates under linear and log-linear combination rules of belief vectors in a distributed hypothesis testing problem. We show that under both combination strategies, agents are able to learn the truth exponentially fast, with a faster rate under log-linear fusion. We examine the gap between the rates in terms of network connectivity and information diversity. We also provide closed-form expressions for special cases involving federated architectures and exchangeable networks.
Social Learning under Randomized Collaborations
Jan 26, 2022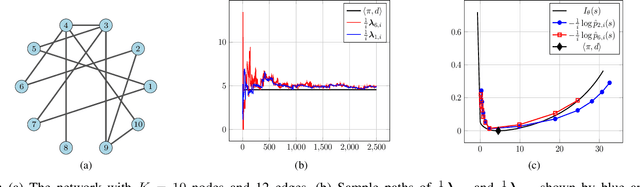
Abstract:We study a social learning scheme where at every time instant, each agent chooses to receive information from one of its neighbors at random. We show that under this sparser communication scheme, the agents learn the truth eventually and the asymptotic convergence rate remains the same as the standard algorithms which use more communication resources. We also derive large deviation estimates of the log-belief ratios for a special case where each agent replaces its belief with that of the chosen neighbor.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge