Integrated Sensing, Communication, and Over-The-Air Control of UAV Swarm Dynamics

Coordinated controlling a large UAV swarm requires significant spectrum resources due to the need for bandwidth allocation per UAV, posing a challenge in resource-limited environments. Over-the-air (OTA) control has emerged as a spectrum-efficient approach, leveraging electromagnetic superposition to form control signals at a base station (BS). However, existing OTA controllers lack sufficient optimization variables to meet UAV swarm control objectives and fail to integrate control with other BS functions like sensing. This work proposes an integrated sensing and OTA control framework (ISAC-OTA) for UAV swarm. The BS performs OTA signal construction (uplink) and dispatch (downlink) while simultaneously sensing objects. Two uplink post-processing methods are developed: a control-centric approach generating closed-form control signals via a feedback-looped OTA control problem, and a sensing-centric method mitigating transmission-induced interference for accurate object sensing. For the downlink, a non-convex problem is formulated and solved to minimize control signal dispatch (transmission) error while maintaining a minimum sensing signal-to-noise ratio (SNR). Simulation results show that the proposed ISAC-OTA controller achieves control performance comparable to the benchmark optimal control algorithm while maintaining high sensing accuracy, despite OTA transmission interference. Moreover, it eliminates the need for per-UAV bandwidth allocation, showcasing a spectrum-efficient method for cooperative control in future wireless systems.

Modelling Networked Dynamical System by Temporal Graph Neural ODE with Irregularly Partial Observed Time-series Data

Modeling the evolution of system with time-series data is a challenging and critical task in a wide range of fields, especially when the time-series data is regularly sampled and partially observable. Some methods have been proposed to estimate the hidden dynamics between intervals like Neural ODE or Exponential decay dynamic function and combine with RNN to estimate the evolution. However, it is difficult for these methods to capture the spatial and temporal dependencies existing within graph-structured time-series data and take full advantage of the available relational information to impute missing data and predict the future states. Besides, traditional RNN-based methods leverage shared RNN cell to update the hidden state which does not capture the impact of various intervals and missing state information on the reliability of estimating the hidden state. To solve this problem, in this paper, we propose a method embedding Graph Neural ODE with reliability and time-aware mechanism which can capture the spatial and temporal dependencies in irregularly sampled and partially observable time-series data to reconstruct the dynamics. Also, a loss function is designed considering the reliability of the augment data from the above proposed method to make further prediction. The proposed method has been validated in experiments of different networked dynamical systems.

Minimize Control Inputs for Strong Structural Controllability Using Reinforcement Learning with Graph Neural Network

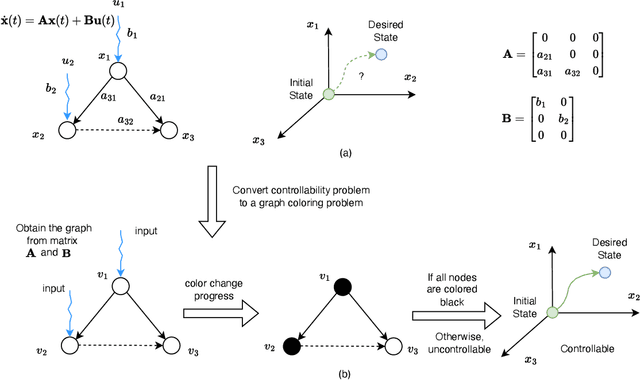
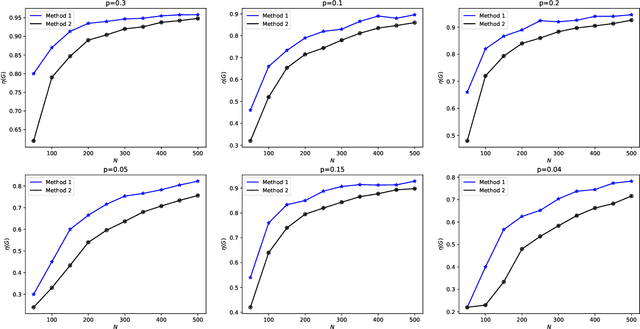
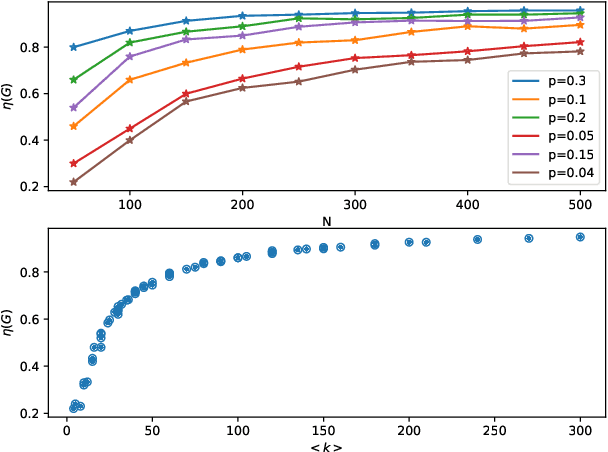
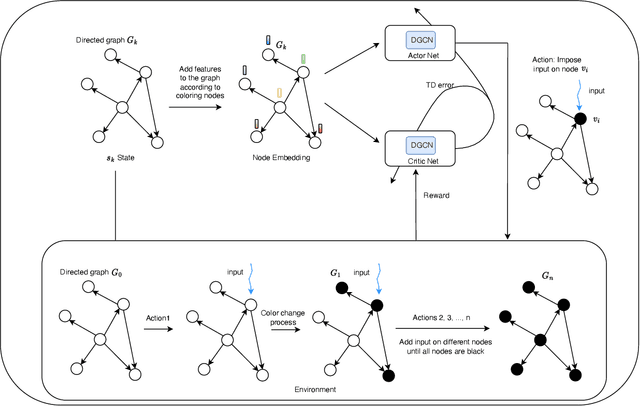
Strong structural controllability (SSC) guarantees networked system with linear-invariant dynamics controllable for all numerical realizations of parameters. Current research has established algebraic and graph-theoretic conditions of SSC for zero/nonzero or zero/nonzero/arbitrary structure. One relevant practical problem is how to fully control the system with the minimal number of input signals and identify which nodes must be imposed signals. Previous work shows that this optimization problem is NP-hard and it is difficult to find the solution. To solve this problem, we formulate the graph coloring process as a Markov decision process (MDP) according to the graph-theoretical condition of SSC for both zero/nonzero and zero/nonzero/arbitrary structure. We use Actor-critic method with Directed graph neural network which represents the color information of graph to optimize MDP. Our method is validated in a social influence network with real data and different complex network models. We find that the number of input nodes is determined by the average degree of the network and the input nodes tend to select nodes with low in-degree and avoid high-degree nodes.