Minimize Control Inputs for Strong Structural Controllability Using Reinforcement Learning with Graph Neural Network
Paper and Code
Feb 26, 2024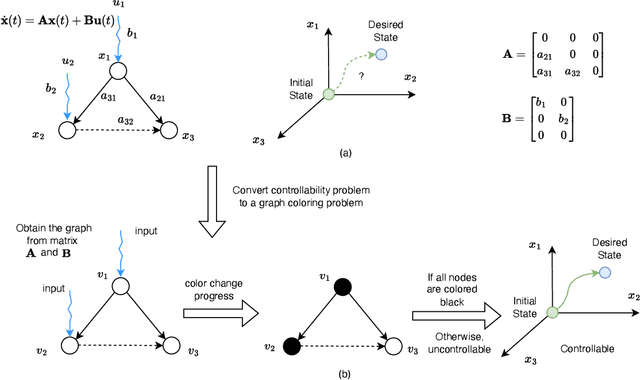
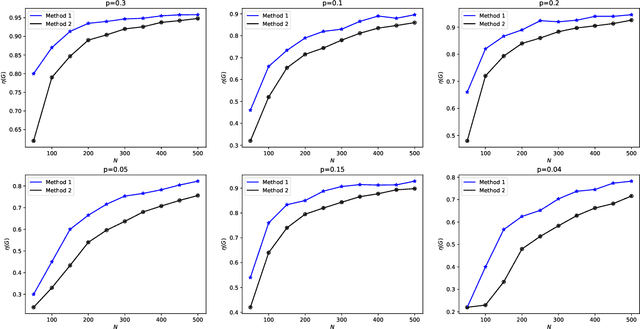
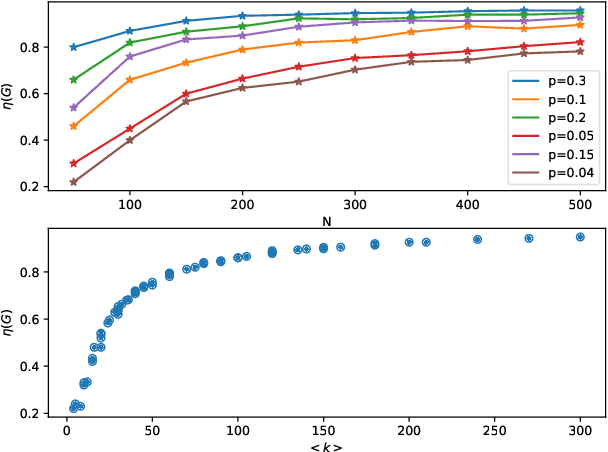
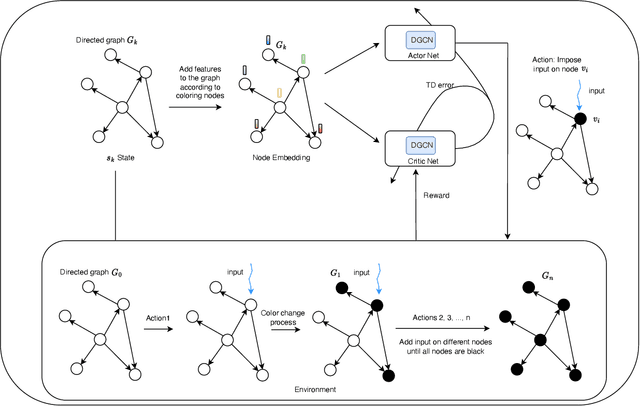
Strong structural controllability (SSC) guarantees networked system with linear-invariant dynamics controllable for all numerical realizations of parameters. Current research has established algebraic and graph-theoretic conditions of SSC for zero/nonzero or zero/nonzero/arbitrary structure. One relevant practical problem is how to fully control the system with the minimal number of input signals and identify which nodes must be imposed signals. Previous work shows that this optimization problem is NP-hard and it is difficult to find the solution. To solve this problem, we formulate the graph coloring process as a Markov decision process (MDP) according to the graph-theoretical condition of SSC for both zero/nonzero and zero/nonzero/arbitrary structure. We use Actor-critic method with Directed graph neural network which represents the color information of graph to optimize MDP. Our method is validated in a social influence network with real data and different complex network models. We find that the number of input nodes is determined by the average degree of the network and the input nodes tend to select nodes with low in-degree and avoid high-degree nodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge