Meiyi Li
Impact of Data Poisoning Attacks on Feasibility and Optimality of Neural Power System Optimizers
Feb 09, 2025Abstract:The increased integration of clean yet stochastic energy resources and the growing number of extreme weather events are narrowing the decision-making window of power grid operators. This time constraint is fueling a plethora of research on Machine Learning-, or ML-, based optimization proxies. While finding a fast solution is appealing, the inherent vulnerabilities of the learning-based methods are hindering their adoption. One of these vulnerabilities is data poisoning attacks, which adds perturbations to ML training data, leading to incorrect decisions. The impact of poisoning attacks on learning-based power system optimizers have not been thoroughly studied, which creates a critical vulnerability. In this paper, we examine the impact of data poisoning attacks on ML-based optimization proxies that are used to solve the DC Optimal Power Flow problem. Specifically, we compare the resilience of three different methods-a penalty-based method, a post-repair approach, and a direct mapping approach-against the adverse effects of poisoning attacks. We will use the optimality and feasibility of these proxies as performance metrics. The insights of this work will establish a foundation for enhancing the resilience of neural power system optimizers.
Toward Rapid, Optimal, and Feasible Power Dispatch through Generalized Neural Mapping
Nov 08, 2023Abstract:The evolution towards a more distributed and interconnected grid necessitates large-scale decision-making within strict temporal constraints. Machine learning (ML) paradigms have demonstrated significant potential in improving the efficacy of optimization processes. However, the feasibility of solutions derived from ML models continues to pose challenges. It's imperative that ML models produce solutions that are attainable and realistic within the given system constraints of power systems. To address the feasibility issue and expedite the solution search process, we proposed LOOP-LC 2.0(Learning to Optimize the Optimization Process with Linear Constraints version 2.0) as a learning-based approach for solving the power dispatch problem. A notable advantage of the LOOP-LC 2.0 framework is its ability to ensure near-optimality and strict feasibility of solutions without depending on computationally intensive post-processing procedures, thus eliminating the need for iterative processes. At the heart of the LOOP-LC 2.0 model lies the newly proposed generalized gauge map method, capable of mapping any infeasible solution to a feasible point within the linearly-constrained domain. The proposed generalized gauge map method improves the traditional gauge map by exhibiting reduced sensitivity to input variances while increasing search speeds significantly. Utilizing the IEEE-200 test case as a benchmark, we demonstrate the effectiveness of the LOOP-LC 2.0 methodology, confirming its superior performance in terms of training speed, computational time, optimality, and solution feasibility compared to existing methodologies.
Machine Learning Infused Distributed Optimization for Coordinating Virtual Power Plant Assets
Oct 27, 2023Abstract:Amid the increasing interest in the deployment of Distributed Energy Resources (DERs), the Virtual Power Plant (VPP) has emerged as a pivotal tool for aggregating diverse DERs and facilitating their participation in wholesale energy markets. These VPP deployments have been fueled by the Federal Energy Regulatory Commission's Order 2222, which makes DERs and VPPs competitive across market segments. However, the diversity and decentralized nature of DERs present significant challenges to the scalable coordination of VPP assets. To address efficiency and speed bottlenecks, this paper presents a novel machine learning-assisted distributed optimization to coordinate VPP assets. Our method, named LOOP-MAC(Learning to Optimize the Optimization Process for Multi-agent Coordination), adopts a multi-agent coordination perspective where each VPP agent manages multiple DERs and utilizes neural network approximators to expedite the solution search. The LOOP-MAC method employs a gauge map to guarantee strict compliance with local constraints, effectively reducing the need for additional post-processing steps. Our results highlight the advantages of LOOP-MAC, showcasing accelerated solution times per iteration and significantly reduced convergence times. The LOOP-MAC method outperforms conventional centralized and distributed optimization methods in optimization tasks that require repetitive and sequential execution.
Teaching Networks to Solve Optimization Problems
Feb 08, 2022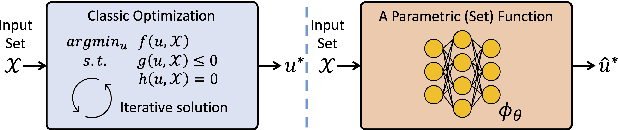
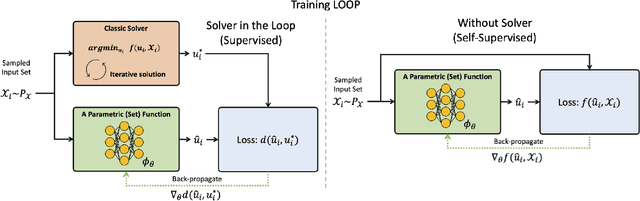
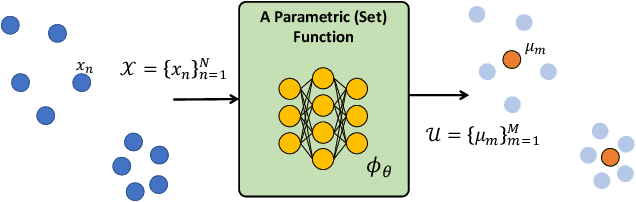
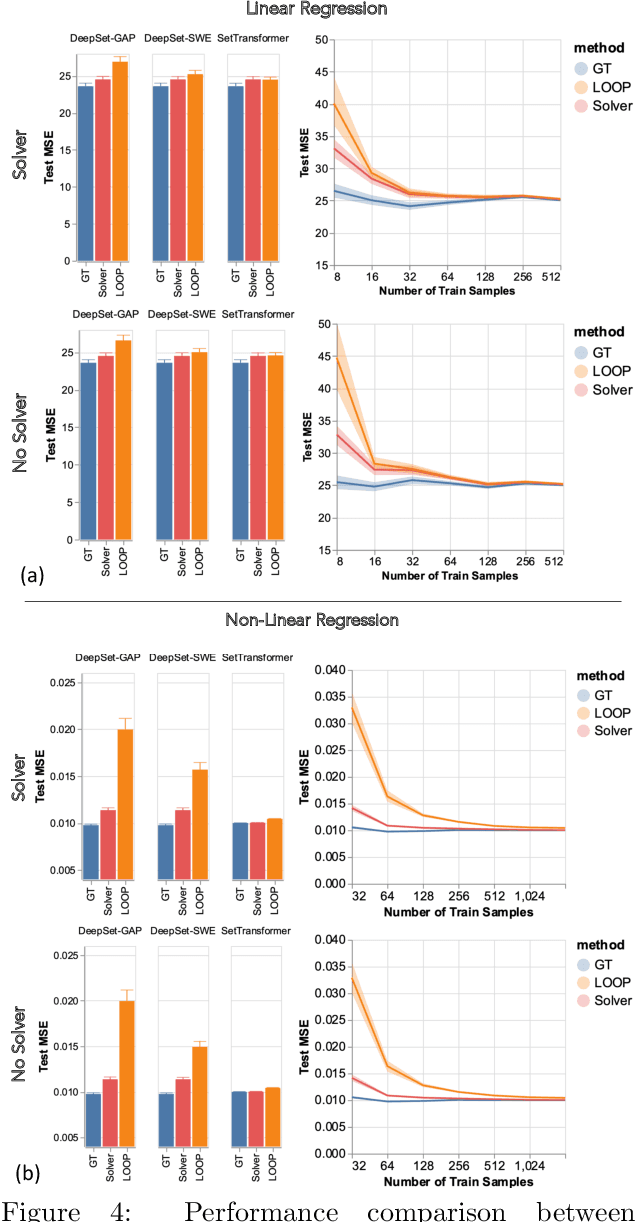
Abstract:Leveraging machine learning to optimize the optimization process is an emerging field which holds the promise to bypass the fundamental computational bottleneck caused by traditional iterative solvers in critical applications requiring near-real-time optimization. The majority of existing approaches focus on learning data-driven optimizers that lead to fewer iterations in solving an optimization. In this paper, we take a different approach and propose to replace the iterative solvers altogether with a trainable parametric set function that outputs the optimal arguments/parameters of an optimization problem in a single feed-forward. We denote our method as, Learning to Optimize the Optimization Process (LOOP). We show the feasibility of learning such parametric (set) functions to solve various classic optimization problems, including linear/nonlinear regression, principal component analysis, transport-based core-set, and quadratic programming in supply management applications. In addition, we propose two alternative approaches for learning such parametric functions, with and without a solver in the-LOOP. Finally, we demonstrate the effectiveness of our proposed approach through various numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge