Unsupervised Evaluation and Weighted Aggregation of Ranked Predictions

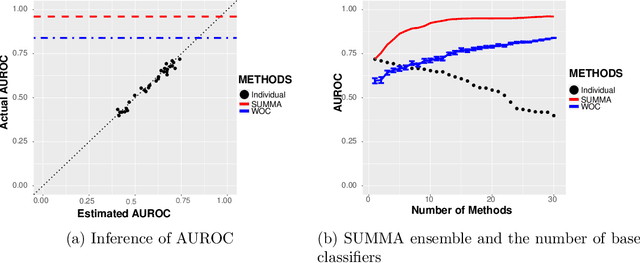
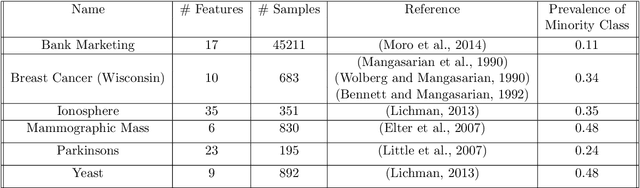
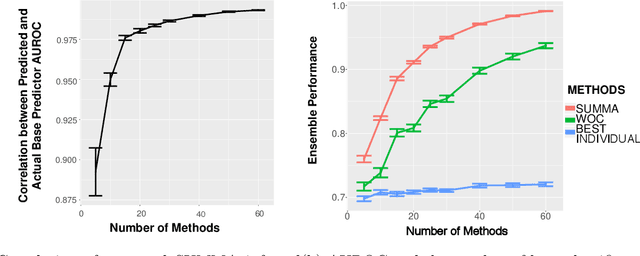
Learning algorithms that aggregate predictions from an ensemble of diverse base classifiers consistently outperform individual methods. Many of these strategies have been developed in a supervised setting, where the accuracy of each base classifier can be empirically measured and this information is incorporated in the training process. However, the reliance on labeled data precludes the application of ensemble methods to many real world problems where labeled data has not been curated. To this end we developed a new theoretical framework for binary classification, the Strategy for Unsupervised Multiple Method Aggregation (SUMMA), to estimate the performances of base classifiers and an optimal strategy for ensemble learning from unlabeled data.

An Approach to One-Bit Compressed Sensing Based on Probably Approximately Correct Learning Theory

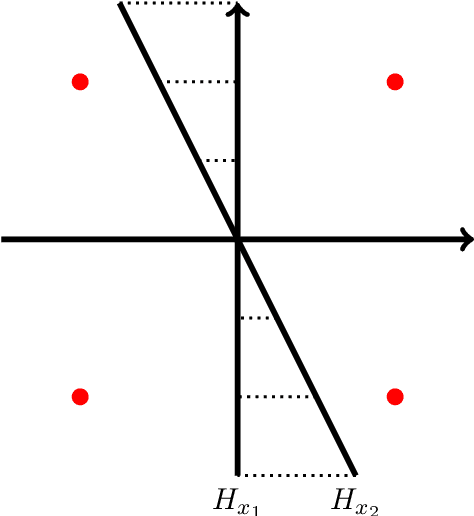
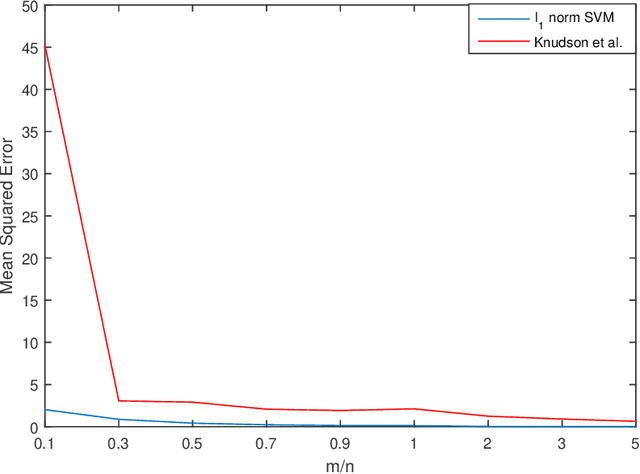
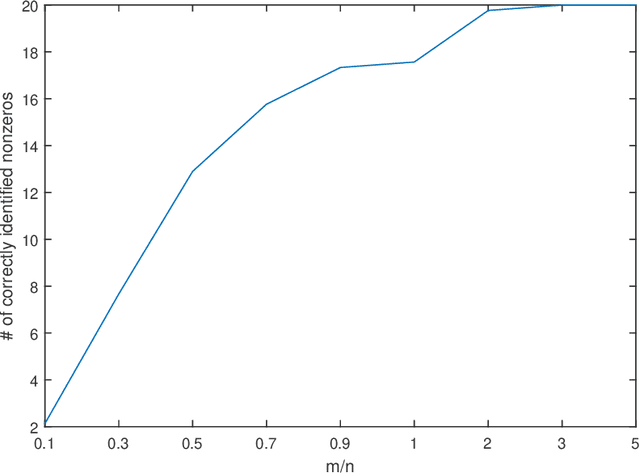
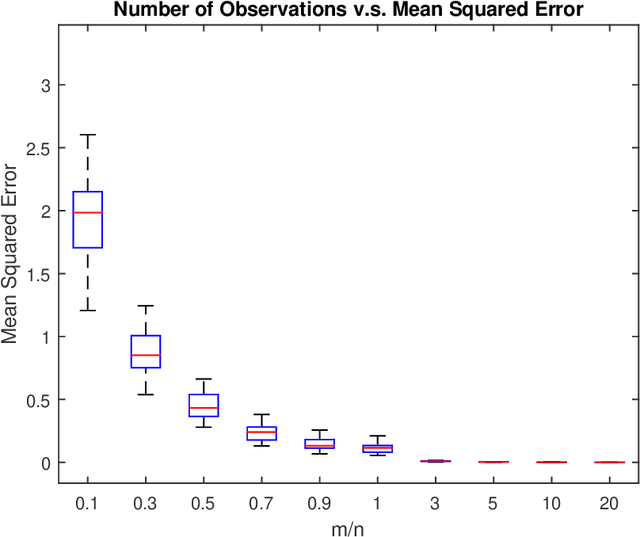
In this paper, the problem of one-bit compressed sensing (OBCS) is formulated as a problem in probably approximately correct (PAC) learning. It is shown that the Vapnik-Chervonenkis (VC-) dimension of the set of half-spaces in $\mathbb{R}^n$ generated by $k$-sparse vectors is bounded below by $k \lg (n/k)$ and above by $2k \lg (n/k)$, plus some round-off terms. By coupling this estimate with well-established results in PAC learning theory, we show that a consistent algorithm can recover a $k$-sparse vector with $O(k \lg (n/k))$ measurements, given only the signs of the measurement vector. This result holds for \textit{all} probability measures on $\mathbb{R}^n$. It is further shown that random sign-flipping errors result only in an increase in the constant in the $O(k \lg (n/k))$ estimate. Because constructing a consistent algorithm is not straight-forward, we present a heuristic based on the $\ell_1$-norm support vector machine, and illustrate that its computational performance is superior to a currently popular method.

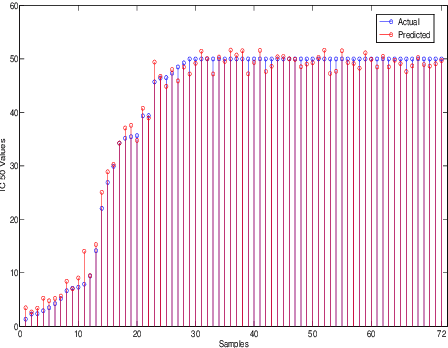
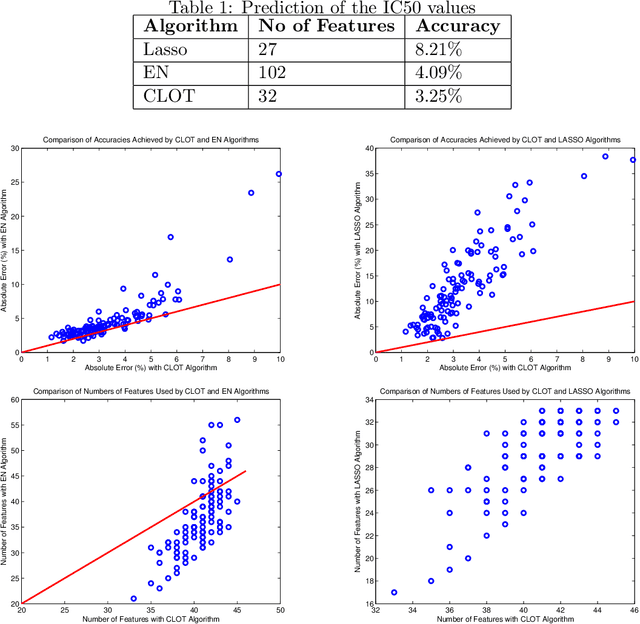
Two New Approaches to Compressed Sensing Exhibiting Both Robust Sparse Recovery and the Grouping Effect

In this paper we introduce a new optimization formulation for sparse regression and compressed sensing, called CLOT (Combined L-One and Two), wherein the regularizer is a convex combination of the $\ell_1$- and $\ell_2$-norms. This formulation differs from the Elastic Net (EN) formulation, in which the regularizer is a convex combination of the $\ell_1$- and $\ell_2$-norm squared. It is shown that, in the context of compressed sensing, the EN formulation does not achieve robust recovery of sparse vectors, whereas the new CLOT formulation achieves robust recovery. Also, like EN but unlike LASSO, the CLOT formulation achieves the grouping effect, wherein coefficients of highly correlated columns of the measurement (or design) matrix are assigned roughly comparable values. It is already known LASSO does not have the grouping effect. Therefore the CLOT formulation combines the best features of both LASSO (robust sparse recovery) and EN (grouping effect). The CLOT formulation is a special case of another one called SGL (Sparse Group LASSO) which was introduced into the literature previously, but without any analysis of either the grouping effect or robust sparse recovery. It is shown here that SGL achieves robust sparse recovery, and also achieves a version of the grouping effect in that coefficients of highly correlated columns belonging to the same group of the measurement (or design) matrix are assigned roughly comparable values.

Near-Ideal Behavior of Compressed Sensing Algorithms

In a recent paper, it is shown that the LASSO algorithm exhibits "near-ideal behavior," in the following sense: Suppose $y = Az + \eta$ where $A$ satisfies the restricted isometry property (RIP) with a sufficiently small constant, and $\Vert \eta \Vert_2 \leq \epsilon$. Then minimizing $\Vert z \Vert_1$ subject to $\Vert y - Az \Vert_2 \leq \epsilon$ leads to an estimate $\hat{x}$ whose error $\Vert \hat{x} - x \Vert_2$ is bounded by a universal constant times the error achieved by an "oracle" that knows the location of the nonzero components of $x$. In the world of optimization, the LASSO algorithm has been generalized in several directions such as the group LASSO, the sparse group LASSO, either without or with tree-structured overlapping groups, and most recently, the sorted LASSO. In this paper, it is shown that {\it any algorithm\/} exhibits near-ideal behavior in the above sense, provided only that (i) the norm used to define the sparsity index is "decomposable," (ii) the penalty norm that is minimized in an effort to enforce sparsity is "$\gamma$-decomposable," and (iii) a "compressibility condition" in terms of a group restricted isometry property is satisfied. Specifically, the group LASSO, and the sparse group LASSO (with some permissible overlap in the groups), as well as the sorted $\ell_1$-norm minimization all exhibit near-ideal behavior. Explicit bounds on the residual error are derived that contain previously known results as special cases.