An Approach to One-Bit Compressed Sensing Based on Probably Approximately Correct Learning Theory
Paper and Code
Oct 22, 2017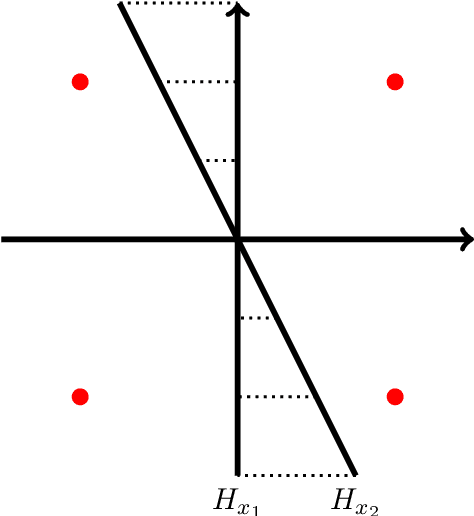
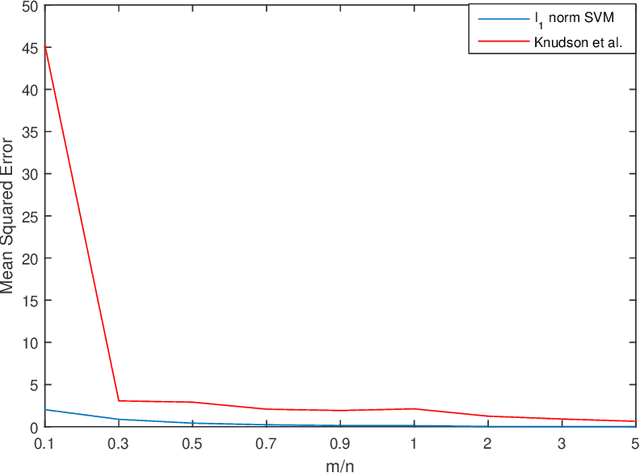
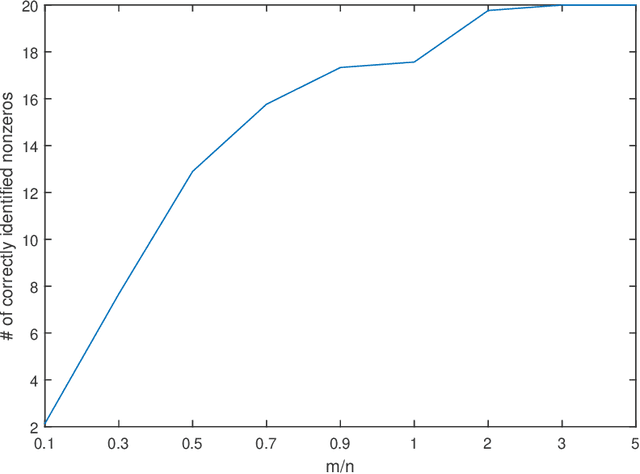
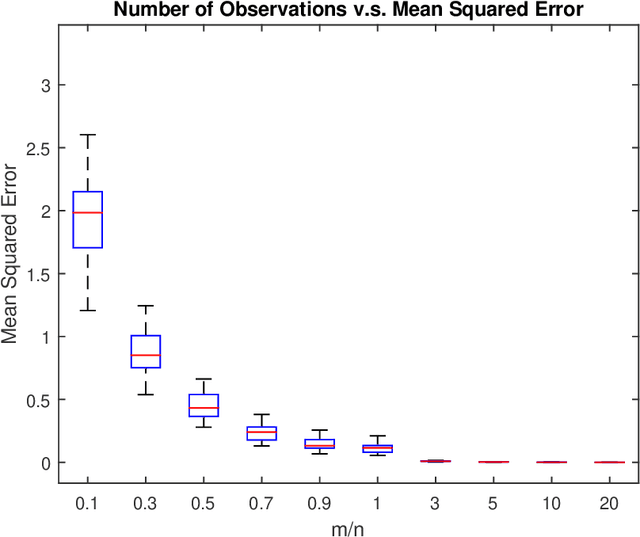
In this paper, the problem of one-bit compressed sensing (OBCS) is formulated as a problem in probably approximately correct (PAC) learning. It is shown that the Vapnik-Chervonenkis (VC-) dimension of the set of half-spaces in $\mathbb{R}^n$ generated by $k$-sparse vectors is bounded below by $k \lg (n/k)$ and above by $2k \lg (n/k)$, plus some round-off terms. By coupling this estimate with well-established results in PAC learning theory, we show that a consistent algorithm can recover a $k$-sparse vector with $O(k \lg (n/k))$ measurements, given only the signs of the measurement vector. This result holds for \textit{all} probability measures on $\mathbb{R}^n$. It is further shown that random sign-flipping errors result only in an increase in the constant in the $O(k \lg (n/k))$ estimate. Because constructing a consistent algorithm is not straight-forward, we present a heuristic based on the $\ell_1$-norm support vector machine, and illustrate that its computational performance is superior to a currently popular method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge