Two New Approaches to Compressed Sensing Exhibiting Both Robust Sparse Recovery and the Grouping Effect
Paper and Code
Jun 20, 2017
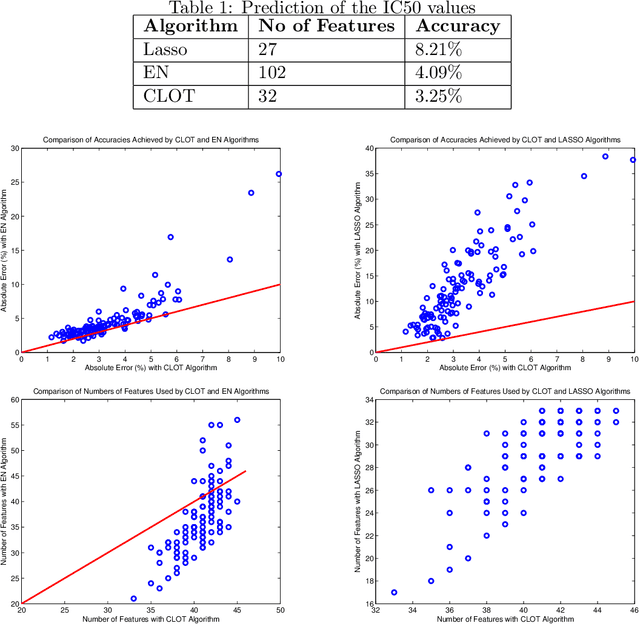
In this paper we introduce a new optimization formulation for sparse regression and compressed sensing, called CLOT (Combined L-One and Two), wherein the regularizer is a convex combination of the $\ell_1$- and $\ell_2$-norms. This formulation differs from the Elastic Net (EN) formulation, in which the regularizer is a convex combination of the $\ell_1$- and $\ell_2$-norm squared. It is shown that, in the context of compressed sensing, the EN formulation does not achieve robust recovery of sparse vectors, whereas the new CLOT formulation achieves robust recovery. Also, like EN but unlike LASSO, the CLOT formulation achieves the grouping effect, wherein coefficients of highly correlated columns of the measurement (or design) matrix are assigned roughly comparable values. It is already known LASSO does not have the grouping effect. Therefore the CLOT formulation combines the best features of both LASSO (robust sparse recovery) and EN (grouping effect). The CLOT formulation is a special case of another one called SGL (Sparse Group LASSO) which was introduced into the literature previously, but without any analysis of either the grouping effect or robust sparse recovery. It is shown here that SGL achieves robust sparse recovery, and also achieves a version of the grouping effect in that coefficients of highly correlated columns belonging to the same group of the measurement (or design) matrix are assigned roughly comparable values.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge