Efficient Network Embedding by Approximate Equitable Partitions

Structural network embedding is a crucial step in enabling effective downstream tasks for complex systems that aims to project a network into a lower-dimensional space while preserving similarities among nodes. We introduce a simple and efficient embedding technique based on approximate variants of equitable partitions. The approximation consists in introducing a user-tunable tolerance parameter relaxing the otherwise strict condition for exact equitable partitions that can be hardly found in real-world networks. We exploit a relationship between equitable partitions and equivalence relations for Markov chains and ordinary differential equations to develop a partition refinement algorithm for computing an approximate equitable partition in polynomial time. We compare our method against state-of-the-art embedding techniques on benchmark networks. We report comparable -- when not superior -- performance for visualization, classification, and regression tasks at a cost between one and three orders of magnitude smaller using a prototype implementation, enabling the embedding of large-scale networks which could not be efficiently handled by most of the competing techniques.

Closed-form Continuous-Depth Models

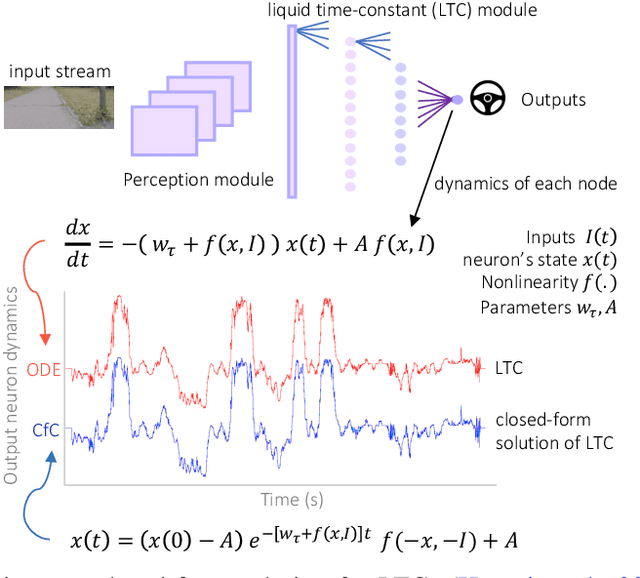
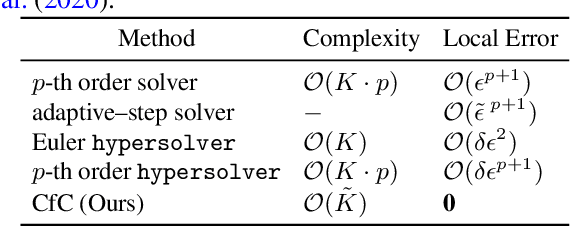
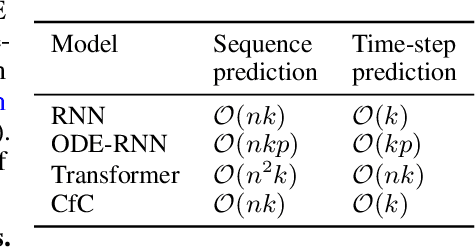
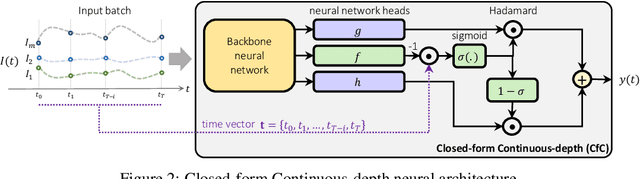
Continuous-depth neural models, where the derivative of the model's hidden state is defined by a neural network, have enabled strong sequential data processing capabilities. However, these models rely on advanced numerical differential equation (DE) solvers resulting in a significant overhead both in terms of computational cost and model complexity. In this paper, we present a new family of models, termed Closed-form Continuous-depth (CfC) networks, that are simple to describe and at least one order of magnitude faster while exhibiting equally strong modeling abilities compared to their ODE-based counterparts. The models are hereby derived from the analytical closed-form solution of an expressive subset of time-continuous models, thus alleviating the need for complex DE solvers all together. In our experimental evaluations, we demonstrate that CfC networks outperform advanced, recurrent models over a diverse set of time-series prediction tasks, including those with long-term dependencies and irregularly sampled data. We believe our findings open new opportunities to train and deploy rich, continuous neural models in resource-constrained settings, which demand both performance and efficiency.