Machine Learning in Falls Prediction; A cognition-based predictor of falls for the acute neurological in-patient population

Background Information: Falls are associated with high direct and indirect costs, and significant morbidity and mortality for patients. Pathological falls are usually a result of a compromised motor system, and/or cognition. Very little research has been conducted on predicting falls based on this premise. Aims: To demonstrate that cognitive and motor tests can be used to create a robust predictive tool for falls. Methods: Three tests of attention and executive function (Stroop, Trail Making, and Semantic Fluency), a measure of physical function (Walk-12), a series of questions (concerning recent falls, surgery and physical function) and demographic information were collected from a cohort of 323 patients at a tertiary neurological center. The principal outcome was a fall during the in-patient stay (n = 54). Data-driven, predictive modelling was employed to identify the statistical modelling strategies which are most accurate in predicting falls, and which yield the most parsimonious models of clinical relevance. Results: The Trail test was identified as the best predictor of falls. Moreover, addition of any others variables, to the results of the Trail test did not improve the prediction (Wilcoxon signed-rank p < .001). The best statistical strategy for predicting falls was the random forest (Wilcoxon signed-rank p < .001), based solely on results of the Trail test. Tuning of the model results in the following optimized values: 68% (+- 7.7) sensitivity, 90% (+- 2.3) specificity, with a positive predictive value of 60%, when the relevant data is available. Conclusion: Predictive modelling has identified a simple yet powerful machine learning prediction strategy based on a single clinical test, the Trail test. Predictive evaluation shows this strategy to be robust, suggesting predictive modelling and machine learning as the standard for future predictive tools.

Varying-coefficient models with isotropic Gaussian process priors

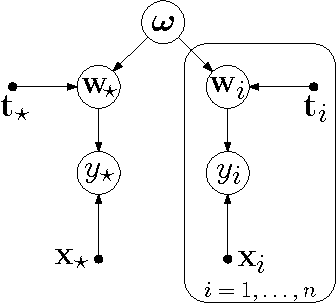
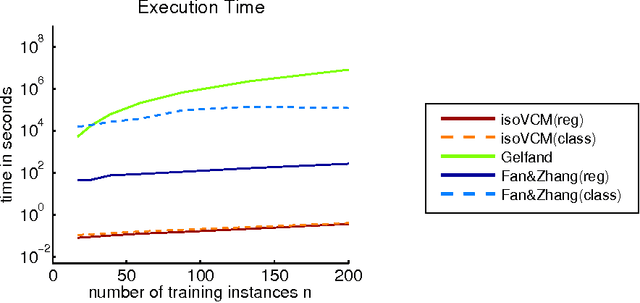
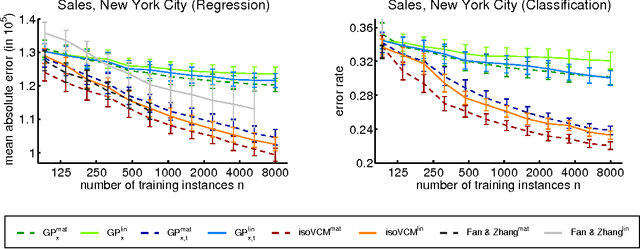
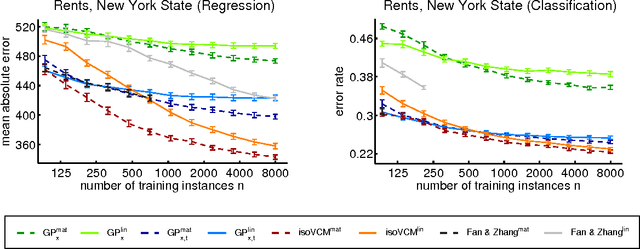
We study learning problems in which the conditional distribution of the output given the input varies as a function of additional task variables. In varying-coefficient models with Gaussian process priors, a Gaussian process generates the functional relationship between the task variables and the parameters of this conditional. Varying-coefficient models subsume hierarchical Bayesian multitask models, but also generalizations in which the conditional varies continuously, for instance, in time or space. However, Bayesian inference in varying-coefficient models is generally intractable. We show that inference for varying-coefficient models with isotropic Gaussian process priors resolves to standard inference for a Gaussian process that can be solved efficiently. MAP inference in this model resolves to multitask learning using task and instance kernels, and inference for hierarchical Bayesian multitask models can be carried out efficiently using graph-Laplacian kernels. We report on experiments for geospatial prediction.