Varying-coefficient models with isotropic Gaussian process priors

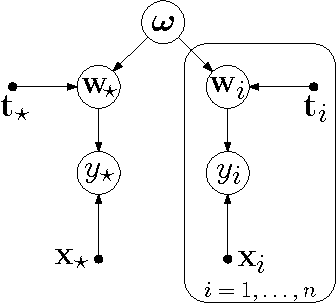
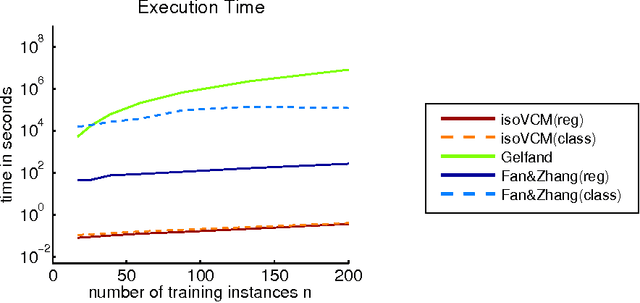
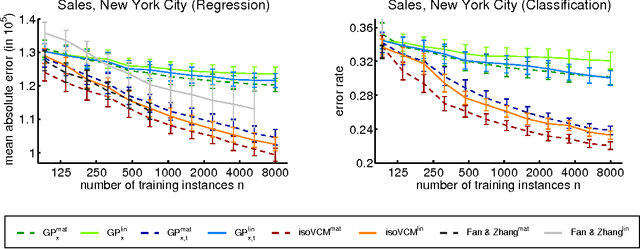
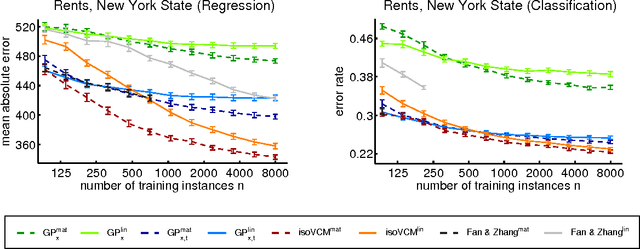
We study learning problems in which the conditional distribution of the output given the input varies as a function of additional task variables. In varying-coefficient models with Gaussian process priors, a Gaussian process generates the functional relationship between the task variables and the parameters of this conditional. Varying-coefficient models subsume hierarchical Bayesian multitask models, but also generalizations in which the conditional varies continuously, for instance, in time or space. However, Bayesian inference in varying-coefficient models is generally intractable. We show that inference for varying-coefficient models with isotropic Gaussian process priors resolves to standard inference for a Gaussian process that can be solved efficiently. MAP inference in this model resolves to multitask learning using task and instance kernels, and inference for hierarchical Bayesian multitask models can be carried out efficiently using graph-Laplacian kernels. We report on experiments for geospatial prediction.

Learning to Identify Regular Expressions that Describe Email Campaigns

This paper addresses the problem of inferring a regular expression from a given set of strings that resembles, as closely as possible, the regular expression that a human expert would have written to identify the language. This is motivated by our goal of automating the task of postmasters of an email service who use regular expressions to describe and blacklist email spam campaigns. Training data contains batches of messages and corresponding regular expressions that an expert postmaster feels confident to blacklist. We model this task as a learning problem with structured output spaces and an appropriate loss function, derive a decoder and the resulting optimization problem, and a report on a case study conducted with an email service.