Transformationally Identical and Invariant Convolutional Neural Networks by Combining Symmetric Operations or Input Vectors

Transformationally invariant processors constructed by transformed input vectors or operators have been suggested and applied to many applications. In this study, transformationally identical processing based on combining results of all sub-processes with corresponding transformations at one of the processing steps or at the beginning step were found to be equivalent for a given condition. This property can be applied to most convolutional neural network (CNN) systems. Specifically, a transformationally identical CNN can be constructed by arranging internally symmetric operations in parallel with the same transformation family that includes a flatten layer with weights sharing among their corresponding transformation elements. Other transformationally identical CNNs can be constructed by averaging transformed input vectors of the family at the input layer followed by an ordinary CNN process or by a set of symmetric operations. Interestingly, we found that both types of transformationally identical CNN systems are mathematically equivalent by either applying an averaging operation to corresponding elements of all sub-channels before the activation function or without using a non-linear activation function.

Geared Rotationally Identical and Invariant Convolutional Neural Network Systems

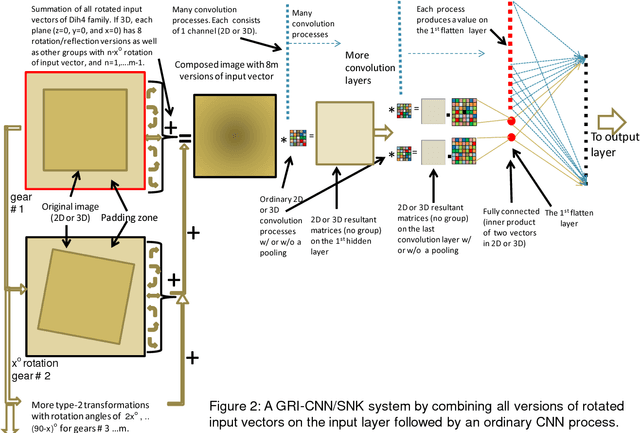
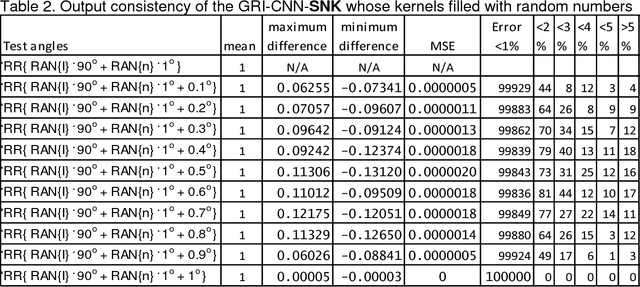
Theorems and techniques to form different types of transformationally invariant processing and to produce the same output quantitatively based on either transformationally invariant operators or symmetric operations have recently been introduced by the authors. In this study, we further propose to compose a geared rotationally identical CNN system (GRI-CNN) with a small step angle by connecting networks of participated processes at the first flatten layer. Using an ordinary CNN structure as a base, requirements for constructing a GRI-CNN include the use of either symmetric input vector or kernels with an angle increment that can form a complete cycle as a "gearwheel". Four basic GRI-CNN structures were studied. Each of them can produce quantitatively identical output results when a rotation angle of the input vector is evenly divisible by the step angle of the gear. Our study showed when an input vector rotated with an angle does not match to a step angle, the GRI-CNN can also produce a highly consistent result. With a design of using an ultra-fine gear-tooth step angle (e.g., 1 degree or 0.1 degree), all four GRI-CNN systems can be constructed virtually isotropically.

Transformationally Identical and Invariant Convolutional Neural Networks through Symmetric Element Operators

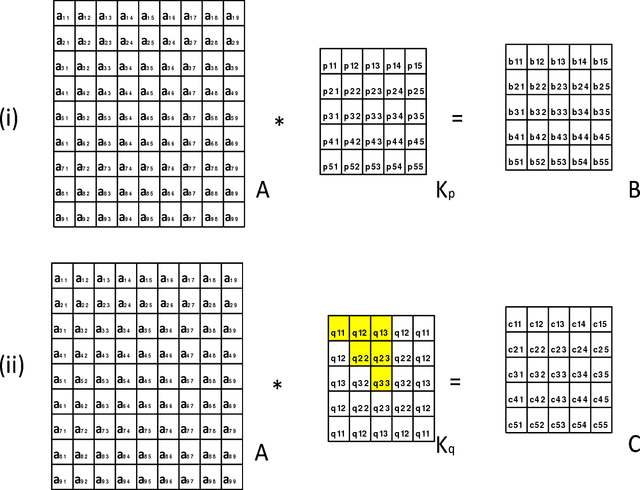
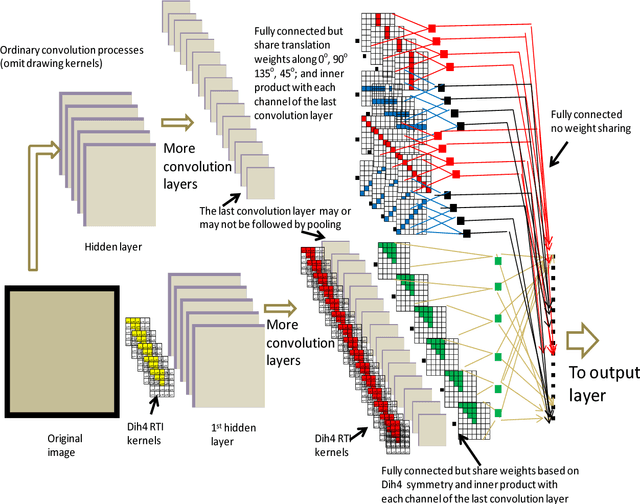
Mathematically speaking, a transformationally invariant operator, such as a transformationally identical (TI) matrix kernel (i.e., K= T{K}), commutes with the transformation (T{.}) itself when they operate on the first operand matrix. We found that by consistently applying the same type of TI kernels in a convolutional neural networks (CNN) system, the commutative property holds throughout all layers of convolution processes with and without involving an activation function and/or a 1D convolution across channels within a layer. We further found that any CNN possessing the same TI kernel property for all convolution layers followed by a flatten layer with weight sharing among their transformation corresponding elements would output the same result for all transformation versions of the original input vector. In short, CNN[ Vi ] = CNN[ T{Vi} ] providing every K = T{K} in CNN, where Vi denotes input vector and CNN[.] represents the whole CNN process as a function of input vector that produces an output vector. With such a transformationally identical CNN (TI-CNN) system, each transformation, that is not associated with a predefined TI used in data augmentation, would inherently include all of its corresponding transformation versions of the input vector for the training. Hence the use of same TI property for every kernel in the CNN would serve as an orientation or a translation independent training guide in conjunction with the error-backpropagation during the training. This TI kernel property is desirable for applications requiring a highly consistent output result from corresponding transformation versions of an input. Several C programming routines are provided to facilitate interested parties of using the TI-CNN technique which is expected to produce a better generalization performance than its ordinary CNN counterpart.