Transformationally Identical and Invariant Convolutional Neural Networks through Symmetric Element Operators

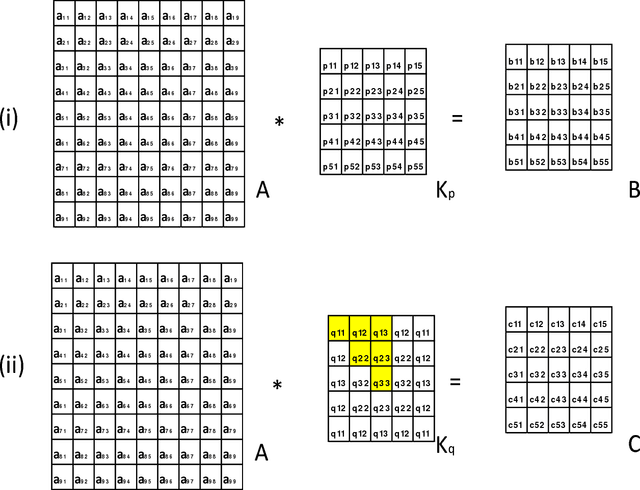
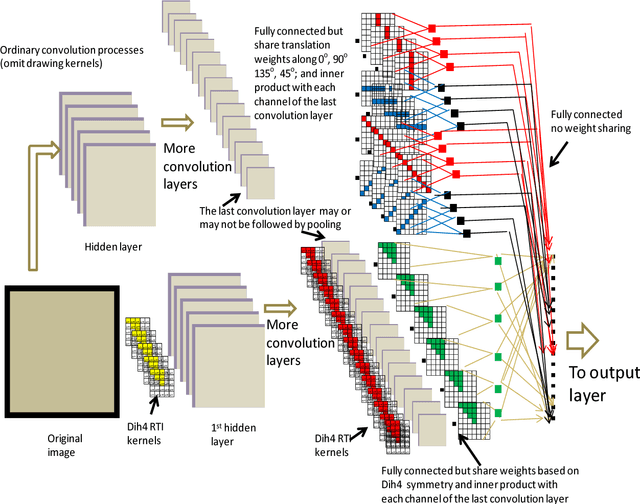
Mathematically speaking, a transformationally invariant operator, such as a transformationally identical (TI) matrix kernel (i.e., K= T{K}), commutes with the transformation (T{.}) itself when they operate on the first operand matrix. We found that by consistently applying the same type of TI kernels in a convolutional neural networks (CNN) system, the commutative property holds throughout all layers of convolution processes with and without involving an activation function and/or a 1D convolution across channels within a layer. We further found that any CNN possessing the same TI kernel property for all convolution layers followed by a flatten layer with weight sharing among their transformation corresponding elements would output the same result for all transformation versions of the original input vector. In short, CNN[ Vi ] = CNN[ T{Vi} ] providing every K = T{K} in CNN, where Vi denotes input vector and CNN[.] represents the whole CNN process as a function of input vector that produces an output vector. With such a transformationally identical CNN (TI-CNN) system, each transformation, that is not associated with a predefined TI used in data augmentation, would inherently include all of its corresponding transformation versions of the input vector for the training. Hence the use of same TI property for every kernel in the CNN would serve as an orientation or a translation independent training guide in conjunction with the error-backpropagation during the training. This TI kernel property is desirable for applications requiring a highly consistent output result from corresponding transformation versions of an input. Several C programming routines are provided to facilitate interested parties of using the TI-CNN technique which is expected to produce a better generalization performance than its ordinary CNN counterpart.