Heang-Ping Chan
Geared Rotationally Identical and Invariant Convolutional Neural Network Systems
Aug 10, 2018

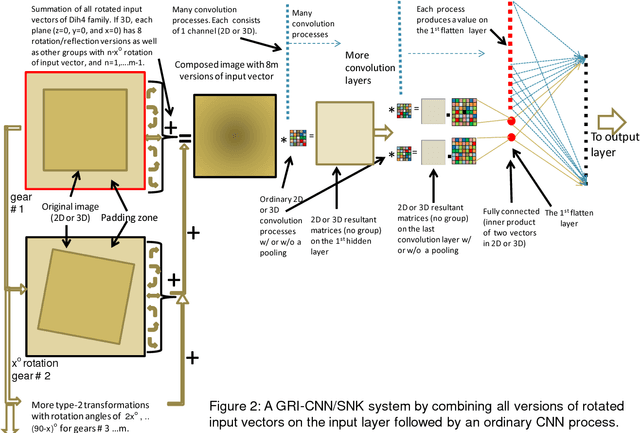
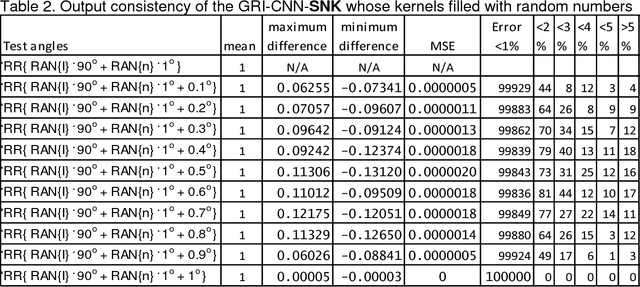
Abstract:Theorems and techniques to form different types of transformationally invariant processing and to produce the same output quantitatively based on either transformationally invariant operators or symmetric operations have recently been introduced by the authors. In this study, we further propose to compose a geared rotationally identical CNN system (GRI-CNN) with a small step angle by connecting networks of participated processes at the first flatten layer. Using an ordinary CNN structure as a base, requirements for constructing a GRI-CNN include the use of either symmetric input vector or kernels with an angle increment that can form a complete cycle as a "gearwheel". Four basic GRI-CNN structures were studied. Each of them can produce quantitatively identical output results when a rotation angle of the input vector is evenly divisible by the step angle of the gear. Our study showed when an input vector rotated with an angle does not match to a step angle, the GRI-CNN can also produce a highly consistent result. With a design of using an ultra-fine gear-tooth step angle (e.g., 1 degree or 0.1 degree), all four GRI-CNN systems can be constructed virtually isotropically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge