Tree-Based Deep Learning for Ranking Symbolic Integration Algorithms

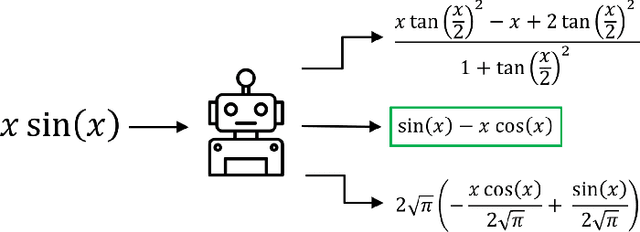
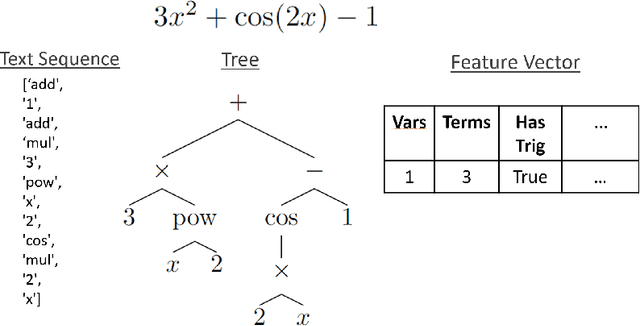
Symbolic indefinite integration in Computer Algebra Systems such as Maple involves selecting the most effective algorithm from multiple available methods. Not all methods will succeed for a given problem, and when several do, the results, though mathematically equivalent, can differ greatly in presentation complexity. Traditionally, this choice has been made with minimal consideration of the problem instance, leading to inefficiencies. We present a machine learning (ML) approach using tree-based deep learning models within a two-stage architecture: first identifying applicable methods for a given instance, then ranking them by predicted output complexity. Furthermore, we find representing mathematical expressions as tree structures significantly improves performance over sequence-based representations, and our two-stage framework outperforms alternative ML formulations. Using a diverse dataset generated by six distinct data generators, our models achieve nearly 90% accuracy in selecting the optimal method on a 70,000 example holdout test set. On an independent out-of-distribution benchmark from Maple's internal test suite, our tree transformer model maintains strong generalisation, outperforming Maple's built-in selector and prior ML approaches. These results highlight the critical role of data representation and problem framing in ML for symbolic computation, and we expect our methodology to generalise effectively to similar optimisation problems in mathematical software.

Transformers to Predict the Applicability of Symbolic Integration Routines

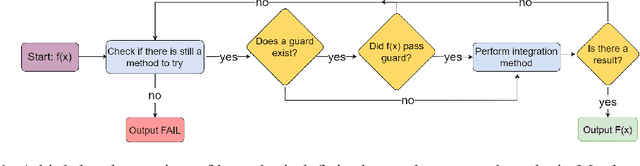
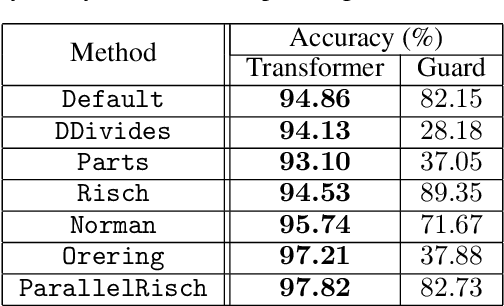
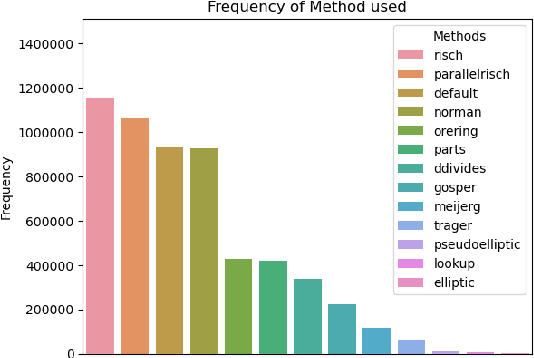
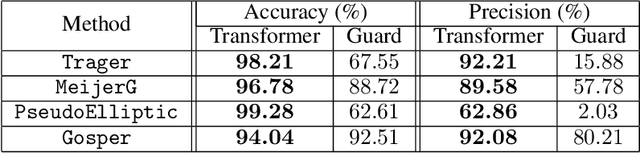
Symbolic integration is a fundamental problem in mathematics: we consider how machine learning may be used to optimise this task in a Computer Algebra System (CAS). We train transformers that predict whether a particular integration method will be successful, and compare against the existing human-made heuristics (called guards) that perform this task in a leading CAS. We find the transformer can outperform these guards, gaining up to 30% accuracy and 70% precision. We further show that the inference time of the transformer is inconsequential which shows that it is well-suited to include as a guard in a CAS. Furthermore, we use Layer Integrated Gradients to interpret the decisions that the transformer is making. If guided by a subject-matter expert, the technique can explain some of the predictions based on the input tokens, which can lead to further optimisations.

The Liouville Generator for Producing Integrable Expressions

There has been a growing need to devise processes that can create comprehensive datasets in the world of Computer Algebra, both for accurate benchmarking and for new intersections with machine learning technology. We present here a method to generate integrands that are guaranteed to be integrable, dubbed the LIOUVILLE method. It is based on Liouville's theorem and the Parallel Risch Algorithm for symbolic integration. We show that this data generation method retains the best qualities of previous data generation methods, while overcoming some of the issues built into that prior work. The LIOUVILLE generator is able to generate sufficiently complex and realistic integrands, and could be used for benchmarking or machine learning training tasks related to symbolic integration.

Constrained Neural Networks for Interpretable Heuristic Creation to Optimise Computer Algebra Systems

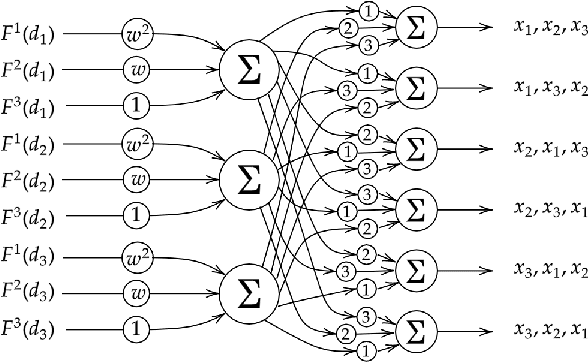
We present a new methodology for utilising machine learning technology in symbolic computation research. We explain how a well known human-designed heuristic to make the choice of variable ordering in cylindrical algebraic decomposition may be represented as a constrained neural network. This allows us to then use machine learning methods to further optimise the heuristic, leading to new networks of similar size, representing new heuristics of similar complexity as the original human-designed one. We present this as a form of ante-hoc explainability for use in computer algebra development.

Symbolic Integration Algorithm Selection with Machine Learning: LSTMs vs Tree LSTMs

Computer Algebra Systems (e.g. Maple) are used in research, education, and industrial settings. One of their key functionalities is symbolic integration, where there are many sub-algorithms to choose from that can affect the form of the output integral, and the runtime. Choosing the right sub-algorithm for a given problem is challenging: we hypothesise that Machine Learning can guide this sub-algorithm choice. A key consideration of our methodology is how to represent the mathematics to the ML model: we hypothesise that a representation which encodes the tree structure of mathematical expressions would be well suited. We trained both an LSTM and a TreeLSTM model for sub-algorithm prediction and compared them to Maple's existing approach. Our TreeLSTM performs much better than the LSTM, highlighting the benefit of using an informed representation of mathematical expressions. It is able to produce better outputs than Maple's current state-of-the-art meta-algorithm, giving a strong basis for further research.

Lessons on Datasets and Paradigms in Machine Learning for Symbolic Computation: A Case Study on CAD

Symbolic Computation algorithms and their implementation in computer algebra systems often contain choices which do not affect the correctness of the output but can significantly impact the resources required: such choices can benefit from having them made separately for each problem via a machine learning model. This study reports lessons on such use of machine learning in symbolic computation, in particular on the importance of analysing datasets prior to machine learning and on the different machine learning paradigms that may be utilised. We present results for a particular case study, the selection of variable ordering for cylindrical algebraic decomposition, but expect that the lessons learned are applicable to other decisions in symbolic computation. We utilise an existing dataset of examples derived from applications which was found to be imbalanced with respect to the variable ordering decision. We introduce an augmentation technique for polynomial systems problems that allows us to balance and further augment the dataset, improving the machine learning results by 28\% and 38\% on average, respectively. We then demonstrate how the existing machine learning methodology used for the problem $-$ classification $-$ might be recast into the regression paradigm. While this does not have a radical change on the performance, it does widen the scope in which the methodology can be applied to make choices.

Data Augmentation for Mathematical Objects

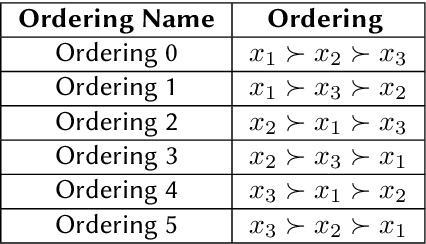
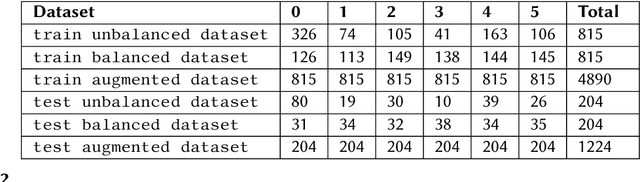
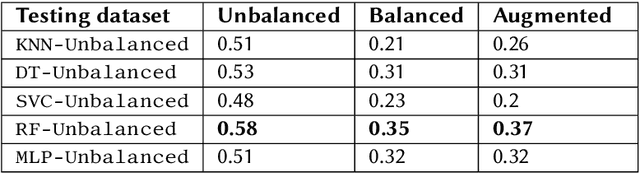
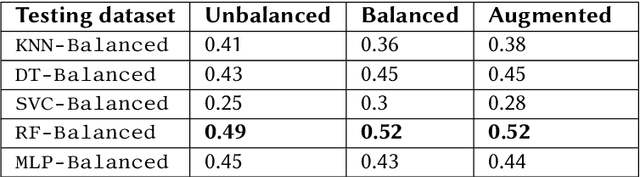
This paper discusses and evaluates ideas of data balancing and data augmentation in the context of mathematical objects: an important topic for both the symbolic computation and satisfiability checking communities, when they are making use of machine learning techniques to optimise their tools. We consider a dataset of non-linear polynomial problems and the problem of selecting a variable ordering for cylindrical algebraic decomposition to tackle these with. By swapping the variable names in already labelled problems, we generate new problem instances that do not require any further labelling when viewing the selection as a classification problem. We find this augmentation increases the accuracy of ML models by 63% on average. We study what part of this improvement is due to the balancing of the dataset and what is achieved thanks to further increasing the size of the dataset, concluding that both have a very significant effect. We finish the paper by reflecting on how this idea could be applied in other uses of machine learning in mathematics.

Generating Elementary Integrable Expressions

There has been an increasing number of applications of machine learning to the field of Computer Algebra in recent years, including to the prominent sub-field of Symbolic Integration. However, machine learning models require an abundance of data for them to be successful and there exist few benchmarks on the scale required. While methods to generate new data already exist, they are flawed in several ways which may lead to bias in machine learning models trained upon them. In this paper, we describe how to use the Risch Algorithm for symbolic integration to create a dataset of elementary integrable expressions. Further, we show that data generated this way alleviates some of the flaws found in earlier methods.

Explainable AI Insights for Symbolic Computation: A case study on selecting the variable ordering for cylindrical algebraic decomposition

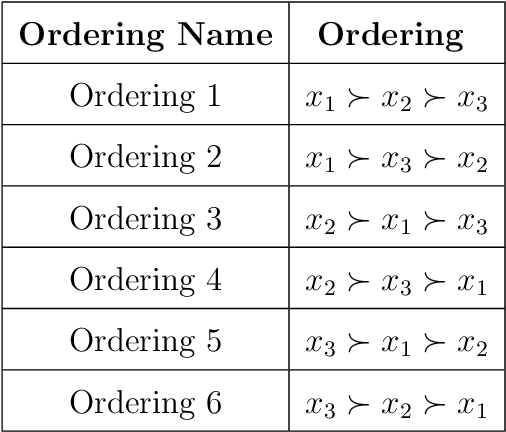
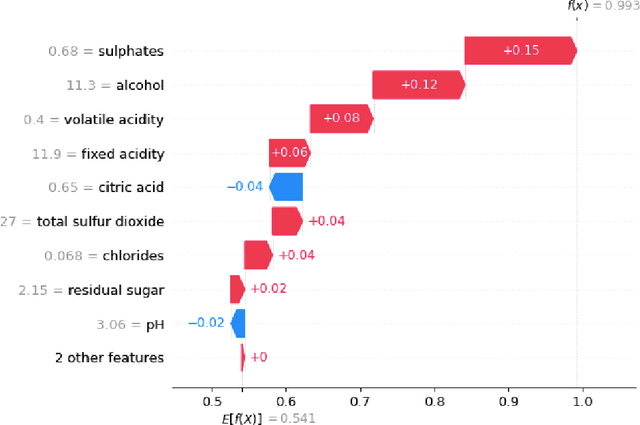
In recent years there has been increased use of machine learning (ML) techniques within mathematics, including symbolic computation where it may be applied safely to optimise or select algorithms. This paper explores whether using explainable AI (XAI) techniques on such ML models can offer new insight for symbolic computation, inspiring new implementations within computer algebra systems that do not directly call upon AI tools. We present a case study on the use of ML to select the variable ordering for cylindrical algebraic decomposition. It has already been demonstrated that ML can make the choice well, but here we show how the SHAP tool for explainability can be used to inform new heuristics of a size and complexity similar to those human-designed heuristics currently commonly used in symbolic computation.

SC-Square: Future Progress with Machine Learning?

The algorithms employed by our communities are often underspecified, and thus have multiple implementation choices, which do not effect the correctness of the output, but do impact the efficiency or even tractability of its production. In this extended abstract, to accompany a keynote talk at the 2021 SC-Square Workshop, we survey recent work (both the author's and from the literature) on the use of Machine Learning technology to improve algorithms of interest to SC-Square.