Constrained Neural Networks for Interpretable Heuristic Creation to Optimise Computer Algebra Systems

We present a new methodology for utilising machine learning technology in symbolic computation research. We explain how a well known human-designed heuristic to make the choice of variable ordering in cylindrical algebraic decomposition may be represented as a constrained neural network. This allows us to then use machine learning methods to further optimise the heuristic, leading to new networks of similar size, representing new heuristics of similar complexity as the original human-designed one. We present this as a form of ante-hoc explainability for use in computer algebra development.

A Generalized Approach for Recovering Time Encoded Signals with Finite Rate of Innovation

In this paper, we consider the problem of recovering a sum of filtered Diracs, representing an input with finite rate of innovation (FRI), from its corresponding time encoding machine (TEM) measurements. So far, the recovery was guaranteed for cases where the filter is selected from a number of particular mathematical functions. Here, we introduce a new generalized method for recovering FRI signals from the TEM output. On the theoretical front, we significantly increase the class of filters for which reconstruction is guaranteed, and provide a condition for perfect input recovery depending on the first two local derivatives of the filter. We extend this result with reconstruction guarantees in the case of noise corrupted FRI signals. On the practical front, in cases where the filter has an unknown mathematical function, the proposed method streamlines the recovery process by bypassing the filter modelling stage. We validate the proposed method via numerical simulations with filters previously used in the literature, as well as filters that are not compatible with the existing results. Additionally, we validate the results using a TEM hardware implementation.

Unlimited Sampling of Bandpass Signals: Computational Demodulation via Undersampling

Bandpass signals are an important sub-class of bandlimited signals that naturally arise in a number of application areas but their high-frequency content poses an acquisition challenge. Consequently, "Bandpass Sampling Theory" has been investigated and applied in the literature. In this paper, we consider the problem of modulo sampling of bandpass signals with the main goal of sampling and recovery of high dynamic range inputs. Our work is inspired by the Unlimited Sensing Framework (USF). In the USF, the modulo operation folds high dynamic range inputs into low dynamic range, modulo samples. This fundamentally avoids signal clipping. Given that the output of the modulo nonlinearity is non-bandlimited, bandpass sampling conditions never hold true. Yet, we show that bandpass signals can be recovered from a modulo representation despite the inevitable aliasing. Our main contribution includes proof of sampling theorems for recovery of bandpass signals from an undersampled representation, reaching sub-Nyquist sampling rates. On the recovery front, by considering both time-and frequency-domain perspectives, we provide a holistic view of the modulo bandpass sampling problem. On the hardware front, we include ideal, non-ideal and generalized modulo folding architectures that arise in the hardware implementation of modulo analog-to-digital converters. Numerical simulations corroborate our theoretical results. Bridging the theory-practice gap, we validate our results using hardware experiments, thus demonstrating the practical effectiveness of our methods.

Multi-Dimensional Unlimited Sampling and Robust Reconstruction

In this paper we introduce a new sampling and reconstruction approach for multi-dimensional analog signals. Building on top of the Unlimited Sensing Framework (USF), we present a new folded sampling operator called the multi-dimensional modulo-hysteresis that is also backwards compatible with the existing one-dimensional modulo operator. Unlike previous approaches, the proposed model is specifically tailored to multi-dimensional signals. In particular, the model uses certain redundancy in dimensions 2 and above, which is exploited for input recovery with robustness. We prove that the new operator is well-defined and its outputs have a bounded dynamic range. For the noiseless case, we derive a theoretically guaranteed input reconstruction approach. When the input is corrupted by Gaussian noise, we exploit redundancy in higher dimensions to provide a bound on the error probability and show this drops to 0 for high enough sampling rates leading to new theoretical guarantees for the noisy case. Our numerical examples corroborate the theoretical results and show that the proposed approach can handle a significantly larger amount of noise compared to USF.

Time Encoding via Unlimited Sampling: Theory, Algorithms and Hardware Validation

An alternative to conventional uniform sampling is that of time encoding, which converts continuous-time signals into streams of trigger times. This gives rise to Event-Driven Sampling (EDS) models. The data-driven nature of EDS acquisition is advantageous in terms of power consumption and time resolution and is inspired by the information representation in biological nervous systems. If an analog signal is outside a predefined dynamic range, then EDS generates a low density of trigger times, which in turn leads to recovery distortion due to aliasing. In this paper, inspired by the Unlimited Sensing Framework (USF), we propose a new EDS architecture that incorporates a modulo nonlinearity prior to acquisition that we refer to as the modulo EDS or MEDS. In MEDS, the modulo nonlinearity folds high dynamic range inputs into low dynamic range amplitudes, thus avoiding recovery distortion. In particular, we consider the asynchronous sigma-delta modulator (ASDM), previously used for low power analog-to-digital conversion. This novel MEDS based acquisition is enabled by a recent generalization of the modulo nonlinearity called modulo-hysteresis. We design a mathematically guaranteed recovery algorithm for bandlimited inputs based on a sampling rate criterion and provide reconstruction error bounds. We go beyond numerical experiments and also provide a first hardware validation of our approach, thus bridging the gap between theory and practice, while corroborating the conceptual underpinnings of our work.

The Surprising Benefits of Hysteresis in Unlimited Sampling: Theory, Algorithms and Experiments

The Unlimited Sensing Framework (USF) was recently introduced to overcome the sensor saturation bottleneck in conventional digital acquisition systems. At its core, the USF allows for high-dynamic-range (HDR) signal reconstruction by converting a continuous-time signal into folded, low-dynamic-range (LDR), modulo samples. HDR reconstruction is then carried out by algorithmic unfolding of the folded samples. In hardware, however, implementing an ideal modulo folding requires careful calibration, analog design and high precision. At the interface of theory and practice, this paper explores a computational sampling strategy that relaxes strict hardware requirements by compensating them via a novel, mathematically guaranteed recovery method. Our starting point is a generalized model for USF. The generalization relies on two new parameters modeling hysteresis and folding transients} in addition to the modulo threshold. Hysteresis accounts for the mismatch between the reset threshold and the amplitude displacement at the folding time and we refer to a continuous transition period in the implementation of a reset as folding transient. Both these effects are motivated by our hardware experiments and also occur in previous, domain-specific applications. We show that the effect of hysteresis is beneficial for the USF and we leverage it to derive the first recovery guarantees in the context of our generalized USF model. Additionally, we show how the proposed recovery can be directly generalized for the case of lower sampling rates. Our theoretical work is corroborated by hardware experiments that are based on a hysteresis enabled, modulo ADC testbed comprising off-the-shelf electronic components. Thus, by capitalizing on a collaboration between hardware and algorithms, our paper enables an end-to-end pipeline for HDR sampling allowing more flexible hardware implementations.

A machine learning based software pipeline to pick the variable ordering for algorithms with polynomial inputs

We are interested in the application of Machine Learning (ML) technology to improve mathematical software. It may seem that the probabilistic nature of ML tools would invalidate the exact results prized by such software, however, the algorithms which underpin the software often come with a range of choices which are good candidates for ML application. We refer to choices which have no effect on the mathematical correctness of the software, but do impact its performance. In the past we experimented with one such choice: the variable ordering to use when building a Cylindrical Algebraic Decomposition (CAD). We used the Python library Scikit-Learn (sklearn) to experiment with different ML models, and developed new techniques for feature generation and hyper-parameter selection. These techniques could easily be adapted for making decisions other than our immediate application of CAD variable ordering. Hence in this paper we present a software pipeline to use sklearn to pick the variable ordering for an algorithm that acts on a polynomial system. The code described is freely available online.

Improved cross-validation for classifiers that make algorithmic choices to minimise runtime without compromising output correctness

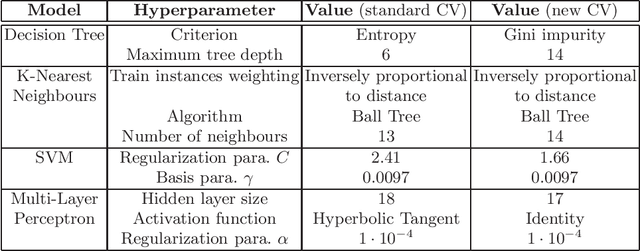
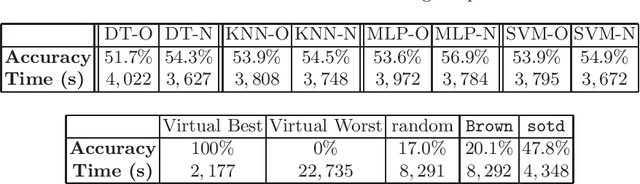
Our topic is the use of machine learning to improve software by making choices which do not compromise the correctness of the output, but do affect the time taken to produce such output. We are particularly concerned with computer algebra systems (CASs), and in particular, our experiments are for selecting the variable ordering to use when performing a cylindrical algebraic decomposition of $n$-dimensional real space with respect to the signs of a set of polynomials. In our prior work we explored the different ML models that could be used, and how to identify suitable features of the input polynomials. In the present paper we both repeat our prior experiments on problems which have more variables (and thus exponentially more possible orderings), and examine the metric which our ML classifiers targets. The natural metric is computational runtime, with classifiers trained to pick the ordering which minimises this. However, this leads to the situation were models do not distinguish between any of the non-optimal orderings, whose runtimes may still vary dramatically. In this paper we investigate a modification to the cross-validation algorithms of the classifiers so that they do distinguish these cases, leading to improved results.

Comparing machine learning models to choose the variable ordering for cylindrical algebraic decomposition

There has been recent interest in the use of machine learning (ML) approaches within mathematical software to make choices that impact on the computing performance without affecting the mathematical correctness of the result. We address the problem of selecting the variable ordering for cylindrical algebraic decomposition (CAD), an important algorithm in Symbolic Computation. Prior work to apply ML on this problem implemented a Support Vector Machine (SVM) to select between three existing human-made heuristics, which did better than anyone heuristic alone. The present work extends to have ML select the variable ordering directly, and to try a wider variety of ML techniques. We experimented with the NLSAT dataset and the Regular Chains Library CAD function for Maple 2018. For each problem, the variable ordering leading to the shortest computing time was selected as the target class for ML. Features were generated from the polynomial input and used to train the following ML models: k-nearest neighbours (KNN) classifier, multi-layer perceptron (MLP), decision tree (DT) and SVM, as implemented in the Python scikit-learn package. We also compared these with the two leading human constructed heuristics for the problem: Brown's heuristic and sotd. On this dataset all of the ML approaches outperformed the human made heuristics, some by a large margin.