Ayush Bhandari
1-Bit Unlimited Sampling Beyond Fourier Domain: Low-Resolution Sampling of Quantization Noise
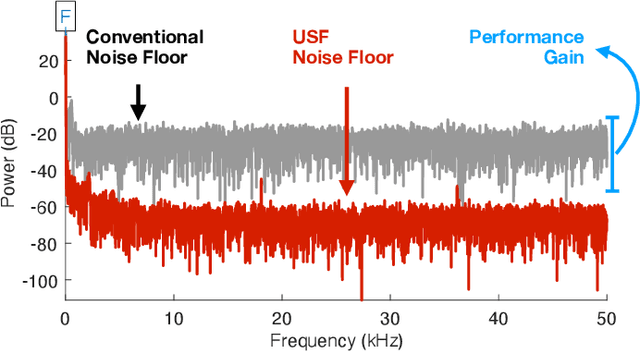
Aug 26, 2025Abstract:Analog-to-digital converters (ADCs) play a critical role in digital signal acquisition across various applications, but their performance is inherently constrained by sampling rates and bit budgets. This bit budget imposes a trade-off between dynamic range (DR) and digital resolution, with ADC energy consumption scaling linearly with sampling rate and exponentially with bit depth. To bypass this, numerous approaches, including oversampling with low-resolution ADCs, have been explored. A prominent example is 1-Bit ADCs with Sigma-Delta Quantization (SDQ), a widely used consumer-grade solution. However, SDQs suffer from overloading or saturation issues, limiting their ability to handle inputs with arbitrary DR. The Unlimited Sensing Framework (USF) addresses this challenge by injecting modulo non-linearity in hardware, resulting in a new digital sensing technology. In this paper, we introduce a novel 1-Bit sampling architecture that extends both conventional 1-Bit SDQ and USF. Our contributions are twofold: (1) We generalize the concept of noise shaping beyond the Fourier domain, allowing the inclusion of non-bandlimited signals in the Fourier domain but bandlimited in alternative transform domains. (2) Building on this generalization, we develop a new transform-domain recovery method for 1-Bit USF. When applied to the Fourier domain, our method demonstrates superior performance compared to existing time-domain techniques, offering reduced oversampling requirements and improved robustness. Extensive numerical experiments validate our findings, laying the groundwork for a broader generalization of 1-Bit sampling systems.
USF Spectral Estimation: Prevalence of Gaussian Cramér-Rao Bounds Despite Modulo Folding
May 06, 2025Abstract:Spectral Estimation (SpecEst) is a core area of signal processing with a history spanning two centuries and applications across various fields. With the advent of digital acquisition, SpecEst algorithms have been widely applied to tasks like frequency super-resolution. However, conventional digital acquisition imposes a trade-off: for a fixed bit budget, one can optimize either signal dynamic range or digital resolution (noise floor), but not both simultaneously. The Unlimited Sensing Framework (USF) overcomes this limitation using modulo non-linearity in analog hardware, enabling a novel approach to SpecEst (USF-SpecEst). However, USF-SpecEst requires new theoretical and algorithmic developments to handle folded samples effectively. In this paper, we derive the Cram\'er-Rao Bounds (CRBs) for SpecEst with noisy modulo-folded samples and reveal a surprising result: the CRBs for USF-SpecEst are scaled versions of the Gaussian CRBs for conventional samples. Numerical experiments validate these bounds, providing a benchmark for USF-SpecEst and facilitating its practical deployment.
Blind Time-of-Flight Imaging: Sparse Deconvolution on the Continuum with Unknown Kernels
Oct 31, 2024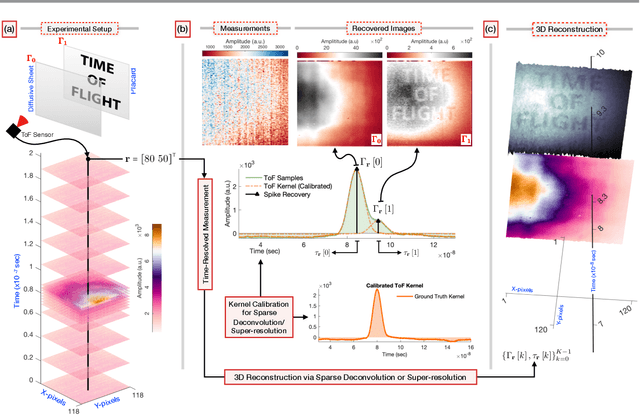



Abstract:In recent years, computational Time-of-Flight (ToF) imaging has emerged as an exciting and a novel imaging modality that offers new and powerful interpretations of natural scenes, with applications extending to 3D, light-in-flight, and non-line-of-sight imaging. Mathematically, ToF imaging relies on algorithmic super-resolution, as the back-scattered sparse light echoes lie on a finer time resolution than what digital devices can capture. Traditional methods necessitate knowledge of the emitted light pulses or kernels and employ sparse deconvolution to recover scenes. Unlike previous approaches, this paper introduces a novel, blind ToF imaging technique that does not require kernel calibration and recovers sparse spikes on a continuum, rather than a discrete grid. By studying the shared characteristics of various ToF modalities, we capitalize on the fact that most physical pulses approximately satisfy the Strang-Fix conditions from approximation theory. This leads to a new mathematical formulation for sparse super-resolution. Our recovery approach uses an optimization method that is pivoted on an alternating minimization strategy. We benchmark our blind ToF method against traditional kernel calibration methods, which serve as the baseline. Extensive hardware experiments across different ToF modalities demonstrate the algorithmic advantages, flexibility and empirical robustness of our approach. We show that our work facilitates super-resolution in scenarios where distinguishing between closely spaced objects is challenging, while maintaining performance comparable to known kernel situations. Examples of light-in-flight imaging and light-sweep videos highlight the practical benefits of our blind super-resolution method in enhancing the understanding of natural scenes.
* 27 pages
Unleashing Dynamic Range and Resolution in Unlimited Sensing Framework via Novel Hardware
Oct 26, 2024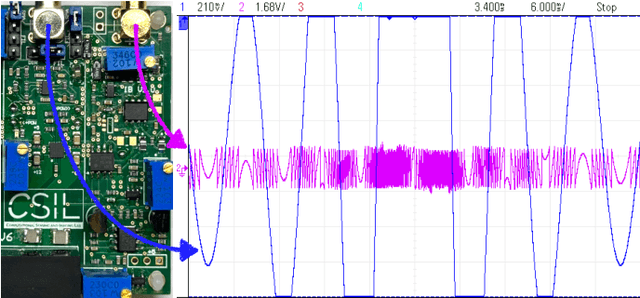
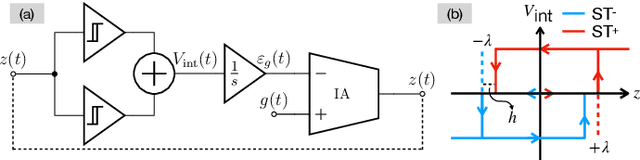
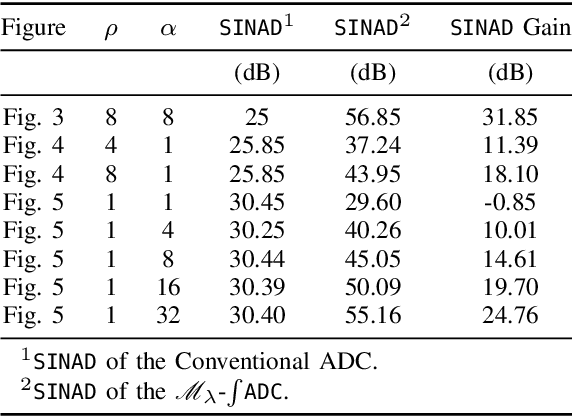
Abstract:Conventional digitization based on the Shannon-Nyquist method, implemented via analog-to-digital converters (ADCs), faces fundamental limitations. High-dynamic-range (HDR) signals often get clipped or saturated in practice. Given a fixed bit budget, one must choose between minimizing quantization noise or accommodating HDR inputs. The Unlimited Sensing Framework (USF) eliminates saturation by incorporating nonlinear folding in analog hardware, resulting in modulo signals. Quantizing or digitizing modulo signals enables low quantization noise as the modulo representation maps HDR signals into low-dynamic-range (LDR) samples. In the context of USF, the core innovation of this paper is a novel, low-cost, integrator-based efficient modulo ADC hardware implementation that imposes no restrictions on folding rates, enabling significantly HDR capture. The feasibility of this design is demonstrated by hardware experiments showcasing clear advantages across different quantitative performance metrics. These include capturing HDR signals with a 60-fold increase in dynamic range, achieving up to 5 Effective Number of Bits (ENOBs), and improving Signal-to-Noise and Distortion (SINAD) by 30 dB.
Sub-Nyquist USF Spectral Estimation: $K$ Frequencies with $6K + 4$ Modulo Samples
Sep 24, 2024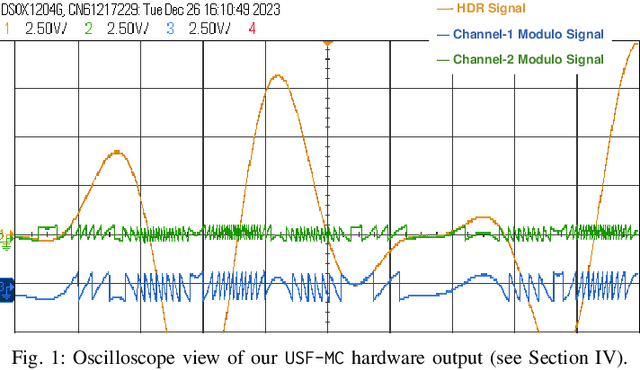
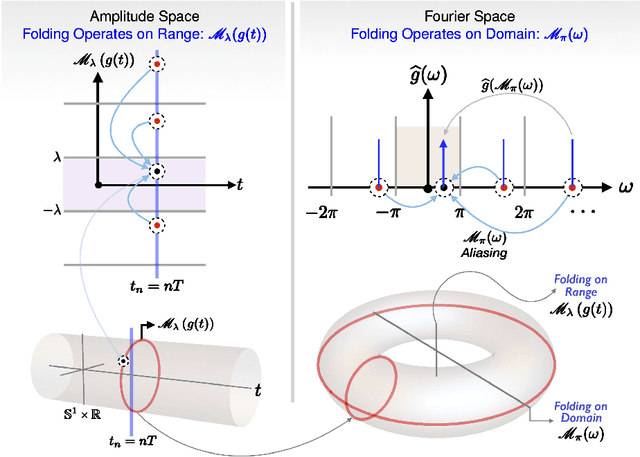
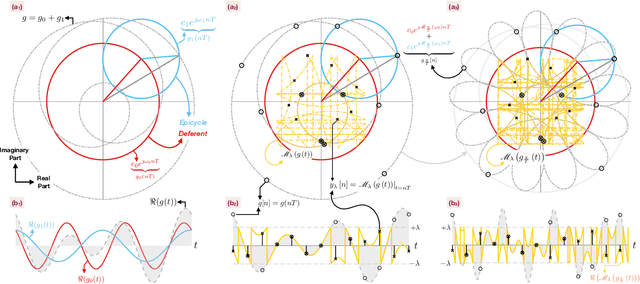
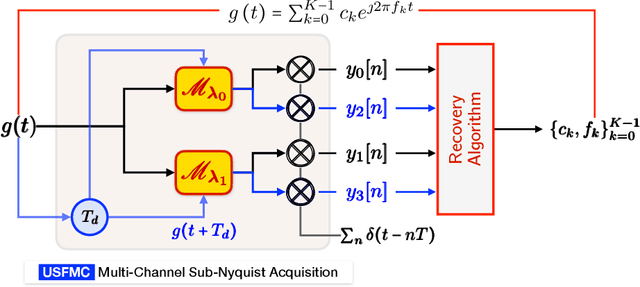
Abstract:Digital acquisition of high bandwidth signals is particularly challenging when Nyquist rate sampling is impractical. This has led to extensive research in sub-Nyquist sampling methods, primarily for spectral and sinusoidal frequency estimation. However, these methods struggle with high-dynamic-range (HDR) signals that can saturate analog-to-digital converters (ADCs). Addressing this, we introduce a novel sub-Nyquist spectral estimation method, driven by the Unlimited Sensing Framework (USF), utilizing a multi-channel system. The sub-Nyquist USF method aliases samples in both amplitude and frequency domains, rendering the inverse problem particularly challenging. Towards this goal, our exact recovery theorem establishes that $K$ sinusoids of arbitrary amplitudes and frequencies can be recovered from $6K + 4$ modulo samples, remarkably, independent of the sampling rate or folding threshold. In the true spirit of sub-Nyquist sampling, via modulo ADC hardware experiments, we demonstrate successful spectrum estimation of HDR signals in the kHz range using Hz range sampling rates (0.078\% Nyquist rate). Our experiments also reveal up to a 33-fold improvement in frequency estimation accuracy using one less bit compared to conventional ADCs. These findings open new avenues in spectral estimation applications, e.g., radars, direction-of-arrival (DoA) estimation, and cognitive radio, showcasing the potential of USF.
Sparse Sampling in Fractional Fourier Domain: Recovery Guarantees and Cramér-Rao Bounds
Apr 29, 2024Abstract:Sampling theory in fractional Fourier Transform (FrFT) domain has been studied extensively in the last decades. This interest stems from the ability of the FrFT to generalize the traditional Fourier Transform, broadening the traditional concept of bandwidth and accommodating a wider range of functions that may not be bandlimited in the Fourier sense. Beyond bandlimited functions, sampling and recovery of sparse signals has also been studied in the FrFT domain. Existing methods for sparse recovery typically operate in the transform domain, capitalizing on the spectral features of spikes in the FrFT domain. Our paper contributes two new theoretical advancements in this area. First, we introduce a novel time-domain sparse recovery method that avoids the typical bottlenecks of transform domain methods, such as spectral leakage. This method is backed by a sparse sampling theorem applicable to arbitrary FrFT-bandlimited kernels and is validated through a hardware experiment. Second, we present Cram\'er-Rao Bounds for the sparse sampling problem, addressing a gap in existing literature.
Full-Duplex Beyond Self-Interference: The Unlimited Sensing Way
Apr 12, 2024Abstract:The success of full-stack full-duplex communication systems depends on how effectively one can achieve digital self-interference cancellation (SIC). Towards this end, in this paper, we consider unlimited sensing framework (USF) enabled full-duplex system. We show that by injecting folding non-linearities in the sensing pipeline, one can not only suppress self-interference but also recover the signal of interest (SoI). This approach leads to novel design of the receiver architecture that is complemented by a modulo-domain channel estimation method. Numerical experiments show that the USF enabled receiver structure can achieve up to 40 dB digital SIC by using as few as 4-bits per sample. Our method outperforms the previous approach based on adaptive filters when it comes to SoI reconstruction, detection, and digital SIC performance.
Fourier-Domain Inversion for the Modulo Radon Transform
Jul 24, 2023Abstract:Inspired by the multiple-exposure fusion approach in computational photography, recently, several practitioners have explored the idea of high dynamic range (HDR) X-ray imaging and tomography. While establishing promising results, these approaches inherit the limitations of multiple-exposure fusion strategy. To overcome these disadvantages, the modulo Radon transform (MRT) has been proposed. The MRT is based on a co-design of hardware and algorithms. In the hardware step, Radon transform projections are folded using modulo non-linearities. Thereon, recovery is performed by algorithmically inverting the folding, thus enabling a single-shot, HDR approach to tomography. The first steps in this topic established rigorous mathematical treatment to the problem of reconstruction from folded projections. This paper takes a step forward by proposing a new, Fourier domain recovery algorithm that is backed by mathematical guarantees. The advantages include recovery at lower sampling rates while being agnostic to modulo threshold, lower computational complexity and empirical robustness to system noise. Beyond numerical simulations, we use prototype modulo ADC based hardware experiments to validate our claims. In particular, we report image recovery based on hardware measurements up to 10 times larger than the sensor's dynamic range while benefiting with lower quantization noise ($\sim$12 dB).
Unlimited Sampling of Bandpass Signals: Computational Demodulation via Undersampling
Jul 10, 2023



Abstract:Bandpass signals are an important sub-class of bandlimited signals that naturally arise in a number of application areas but their high-frequency content poses an acquisition challenge. Consequently, "Bandpass Sampling Theory" has been investigated and applied in the literature. In this paper, we consider the problem of modulo sampling of bandpass signals with the main goal of sampling and recovery of high dynamic range inputs. Our work is inspired by the Unlimited Sensing Framework (USF). In the USF, the modulo operation folds high dynamic range inputs into low dynamic range, modulo samples. This fundamentally avoids signal clipping. Given that the output of the modulo nonlinearity is non-bandlimited, bandpass sampling conditions never hold true. Yet, we show that bandpass signals can be recovered from a modulo representation despite the inevitable aliasing. Our main contribution includes proof of sampling theorems for recovery of bandpass signals from an undersampled representation, reaching sub-Nyquist sampling rates. On the recovery front, by considering both time-and frequency-domain perspectives, we provide a holistic view of the modulo bandpass sampling problem. On the hardware front, we include ideal, non-ideal and generalized modulo folding architectures that arise in the hardware implementation of modulo analog-to-digital converters. Numerical simulations corroborate our theoretical results. Bridging the theory-practice gap, we validate our results using hardware experiments, thus demonstrating the practical effectiveness of our methods.
Unlimited Sampling Radar: a Real-Time End-to-End Demonstrator
Jun 30, 2023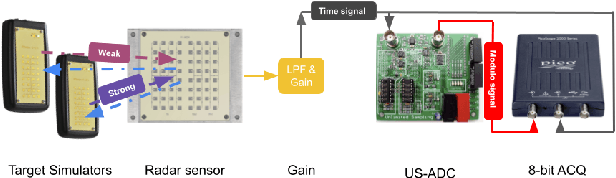
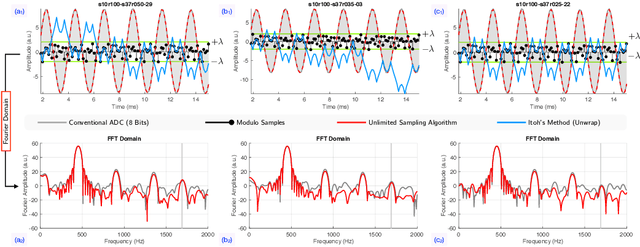
Abstract:In this paper, the trade-off between the quantization noise and the dynamic range of ADCs used to acquire radar signals is revisited using the Unlimited Sensing Framework (USF) in a practical setting. Trade-offs between saturation and resolution arise in many applications, like radar, where sensors acquire signals which exhibit a high degree of variability in amplitude. To solve this issue, we propose the use of the co-design approach of the USF which acquires folded version of the signal of interest and leverages its structure to reconstruct it after its acquisition. We demonstrate that this method outperforms other standard acquisition methods for Doppler radars. Taking our theory all the way to practice, we develop a prototype USF-enabled Doppler Radar and show the clear benefits of our method. In each experiment, we show that using the USF increases sensitivity compared to a classic acquisition approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge