Tereso del Rio
Data Augmentation for Mathematical Objects
Jul 13, 2023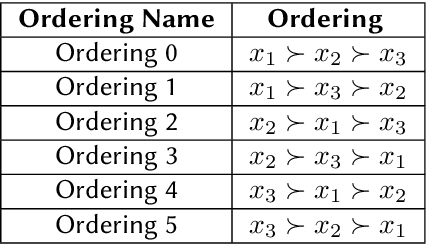
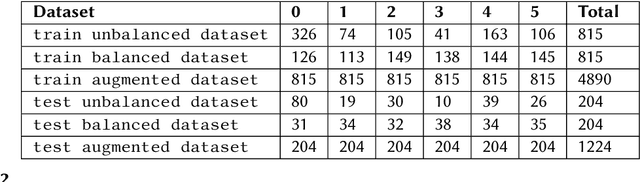
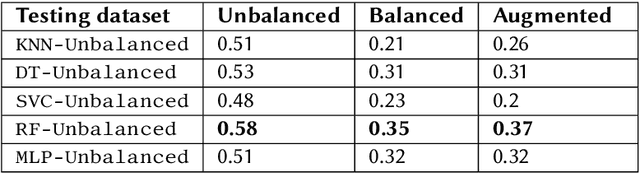
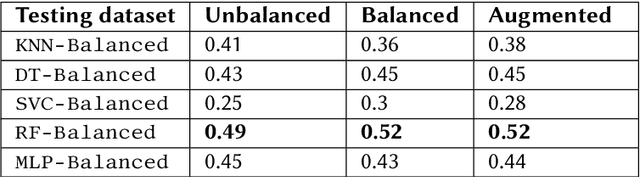
Abstract:This paper discusses and evaluates ideas of data balancing and data augmentation in the context of mathematical objects: an important topic for both the symbolic computation and satisfiability checking communities, when they are making use of machine learning techniques to optimise their tools. We consider a dataset of non-linear polynomial problems and the problem of selecting a variable ordering for cylindrical algebraic decomposition to tackle these with. By swapping the variable names in already labelled problems, we generate new problem instances that do not require any further labelling when viewing the selection as a classification problem. We find this augmentation increases the accuracy of ML models by 63% on average. We study what part of this improvement is due to the balancing of the dataset and what is achieved thanks to further increasing the size of the dataset, concluding that both have a very significant effect. We finish the paper by reflecting on how this idea could be applied in other uses of machine learning in mathematics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge