Rashid Barket
Tree-Based Deep Learning for Ranking Symbolic Integration Algorithms
Aug 08, 2025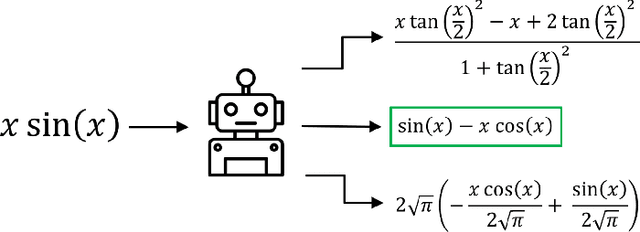

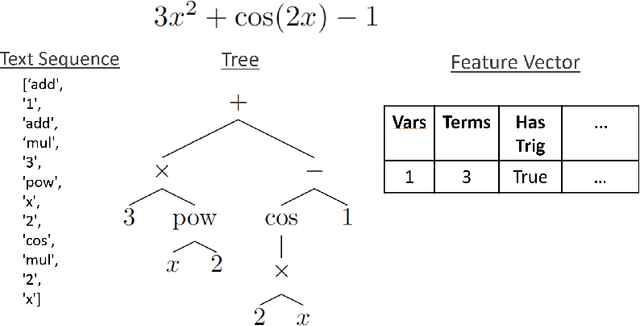

Abstract:Symbolic indefinite integration in Computer Algebra Systems such as Maple involves selecting the most effective algorithm from multiple available methods. Not all methods will succeed for a given problem, and when several do, the results, though mathematically equivalent, can differ greatly in presentation complexity. Traditionally, this choice has been made with minimal consideration of the problem instance, leading to inefficiencies. We present a machine learning (ML) approach using tree-based deep learning models within a two-stage architecture: first identifying applicable methods for a given instance, then ranking them by predicted output complexity. Furthermore, we find representing mathematical expressions as tree structures significantly improves performance over sequence-based representations, and our two-stage framework outperforms alternative ML formulations. Using a diverse dataset generated by six distinct data generators, our models achieve nearly 90% accuracy in selecting the optimal method on a 70,000 example holdout test set. On an independent out-of-distribution benchmark from Maple's internal test suite, our tree transformer model maintains strong generalisation, outperforming Maple's built-in selector and prior ML approaches. These results highlight the critical role of data representation and problem framing in ML for symbolic computation, and we expect our methodology to generalise effectively to similar optimisation problems in mathematical software.
Transformers to Predict the Applicability of Symbolic Integration Routines
Oct 31, 2024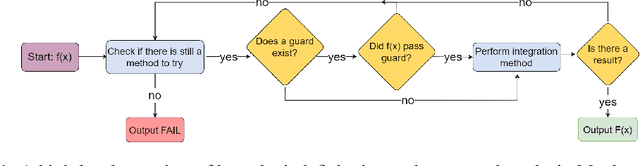
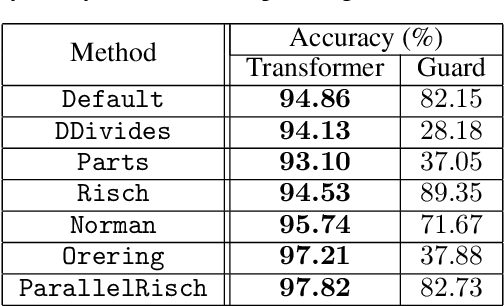
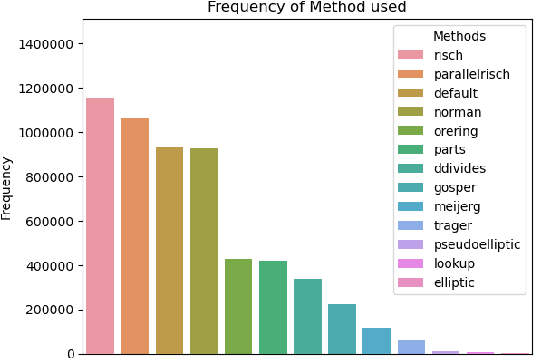
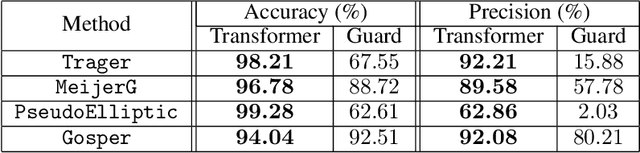
Abstract:Symbolic integration is a fundamental problem in mathematics: we consider how machine learning may be used to optimise this task in a Computer Algebra System (CAS). We train transformers that predict whether a particular integration method will be successful, and compare against the existing human-made heuristics (called guards) that perform this task in a leading CAS. We find the transformer can outperform these guards, gaining up to 30% accuracy and 70% precision. We further show that the inference time of the transformer is inconsequential which shows that it is well-suited to include as a guard in a CAS. Furthermore, we use Layer Integrated Gradients to interpret the decisions that the transformer is making. If guided by a subject-matter expert, the technique can explain some of the predictions based on the input tokens, which can lead to further optimisations.
The Liouville Generator for Producing Integrable Expressions
Jun 17, 2024Abstract:There has been a growing need to devise processes that can create comprehensive datasets in the world of Computer Algebra, both for accurate benchmarking and for new intersections with machine learning technology. We present here a method to generate integrands that are guaranteed to be integrable, dubbed the LIOUVILLE method. It is based on Liouville's theorem and the Parallel Risch Algorithm for symbolic integration. We show that this data generation method retains the best qualities of previous data generation methods, while overcoming some of the issues built into that prior work. The LIOUVILLE generator is able to generate sufficiently complex and realistic integrands, and could be used for benchmarking or machine learning training tasks related to symbolic integration.
Symbolic Integration Algorithm Selection with Machine Learning: LSTMs vs Tree LSTMs
Apr 23, 2024



Abstract:Computer Algebra Systems (e.g. Maple) are used in research, education, and industrial settings. One of their key functionalities is symbolic integration, where there are many sub-algorithms to choose from that can affect the form of the output integral, and the runtime. Choosing the right sub-algorithm for a given problem is challenging: we hypothesise that Machine Learning can guide this sub-algorithm choice. A key consideration of our methodology is how to represent the mathematics to the ML model: we hypothesise that a representation which encodes the tree structure of mathematical expressions would be well suited. We trained both an LSTM and a TreeLSTM model for sub-algorithm prediction and compared them to Maple's existing approach. Our TreeLSTM performs much better than the LSTM, highlighting the benefit of using an informed representation of mathematical expressions. It is able to produce better outputs than Maple's current state-of-the-art meta-algorithm, giving a strong basis for further research.
Generating Elementary Integrable Expressions
Jun 27, 2023Abstract:There has been an increasing number of applications of machine learning to the field of Computer Algebra in recent years, including to the prominent sub-field of Symbolic Integration. However, machine learning models require an abundance of data for them to be successful and there exist few benchmarks on the scale required. While methods to generate new data already exist, they are flawed in several ways which may lead to bias in machine learning models trained upon them. In this paper, we describe how to use the Risch Algorithm for symbolic integration to create a dataset of elementary integrable expressions. Further, we show that data generated this way alleviates some of the flaws found in earlier methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge