IntraSeismic: a coordinate-based learning approach to seismic inversion

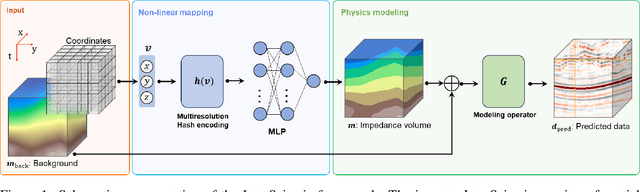
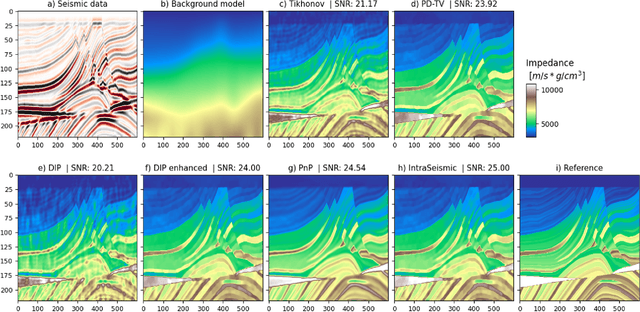
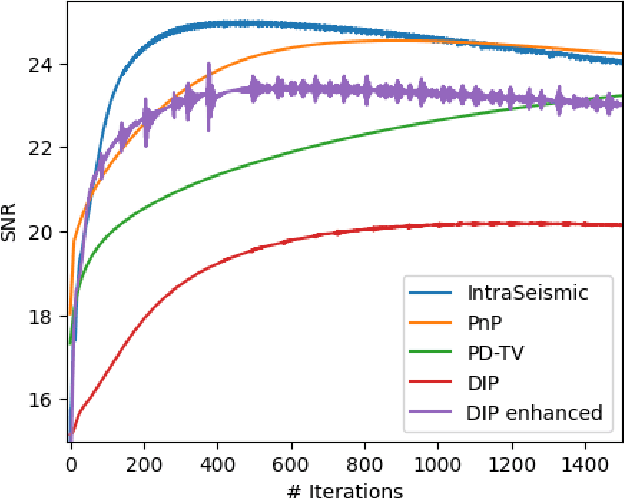
Seismic imaging is the numerical process of creating a volumetric representation of the subsurface geological structures from elastic waves recorded at the surface of the Earth. As such, it is widely utilized in the energy and construction sectors for applications ranging from oil and gas prospection, to geothermal production and carbon capture and storage monitoring, to geotechnical assessment of infrastructures. Extracting quantitative information from seismic recordings, such as an acoustic impedance model, is however a highly ill-posed inverse problem, due to the band-limited and noisy nature of the data. This paper introduces IntraSeismic, a novel hybrid seismic inversion method that seamlessly combines coordinate-based learning with the physics of the post-stack modeling operator. Key features of IntraSeismic are i) unparalleled performance in 2D and 3D post-stack seismic inversion, ii) rapid convergence rates, iii) ability to seamlessly include hard constraints (i.e., well data) and perform uncertainty quantification, and iv) potential data compression and fast randomized access to portions of the inverted model. Synthetic and field data applications of IntraSeismic are presented to validate the effectiveness of the proposed method.

Explainable Artificial Intelligence driven mask design for self-supervised seismic denoising

The presence of coherent noise in seismic data leads to errors and uncertainties, and as such it is paramount to suppress noise as early and efficiently as possible. Self-supervised denoising circumvents the common requirement of deep learning procedures of having noisy-clean training pairs. However, self-supervised coherent noise suppression methods require extensive knowledge of the noise statistics. We propose the use of explainable artificial intelligence approaches to see inside the black box that is the denoising network and use the gained knowledge to replace the need for any prior knowledge of the noise itself. This is achieved in practice by leveraging bias-free networks and the direct linear link between input and output provided by the associated Jacobian matrix; we show that a simple averaging of the Jacobian contributions over a number of randomly selected input pixels, provides an indication of the most effective mask to suppress noise present in the data. The proposed method therefore becomes a fully automated denoising procedure requiring no clean training labels or prior knowledge. Realistic synthetic examples with noise signals of varying complexities, ranging from simple time-correlated noise to complex pseudo rig noise propagating at the velocity of the ocean, are used to validate the proposed approach. Its automated nature is highlighted further by an application to two field datasets. Without any substantial pre-processing or any knowledge of the acquisition environment, the automatically identified blind-masks are shown to perform well in suppressing both trace-wise noise in common shot gathers from the Volve marine dataset and colored noise in post stack seismic images from a land seismic survey.

PINNslope: seismic data interpolation and local slope estimation with physics informed neural networks

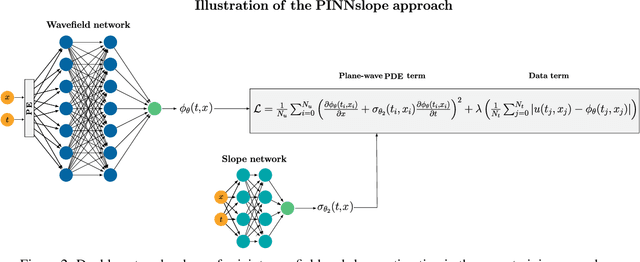
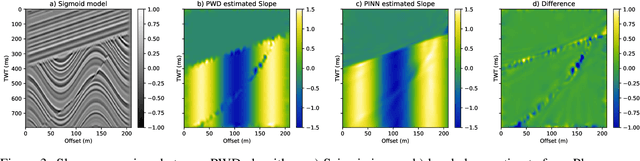
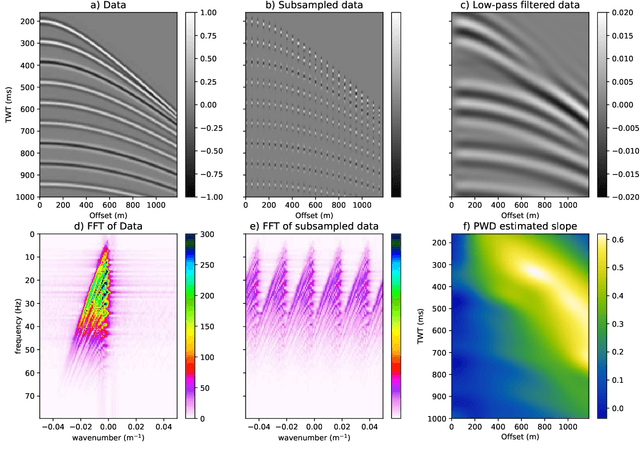
Interpolation of aliased seismic data constitutes a key step in a seismic processing workflow to obtain high quality velocity models and seismic images. Leveraging on the idea of describing seismic wavefields as a superposition of local plane waves, we propose to interpolate seismic data by utilizing a physics informed neural network (PINN). In the proposed framework, two feed-forward neural networks are jointly trained using the local plane wave differential equation as well as the available data as two terms in the objective function: a primary network assisted by positional encoding is tasked with reconstructing the seismic data, whilst an auxiliary, smaller network estimates the associated local slopes. Results on synthetic and field data validate the effectiveness of the proposed method in handling aliased (sampled coarsely) data and data with large gaps. Our method compares favorably against a classic least-squares inversion approach regularized by the local plane-wave equation as well as a PINN-based approach with a single network and pre-computed local slopes. We find that by introducing a second network to estimate the local slopes whilst at the same time interpolating the aliased data, the overall reconstruction capabilities and convergence behavior of the primary network is enhanced. An additional positional encoding, embedded as a network layer, confers to the network the ability to converge faster improving the accuracy of the data term.

Posterior sampling with CNN-based, Plug-and-Play regularization with applications to Post-Stack Seismic Inversion

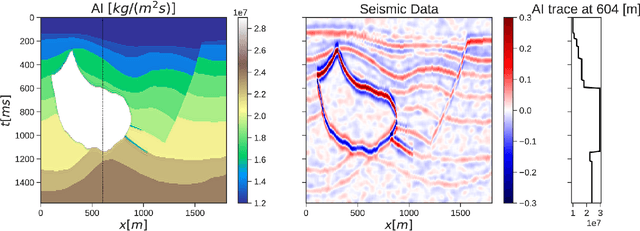
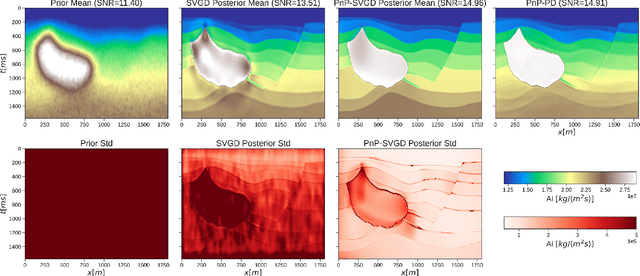
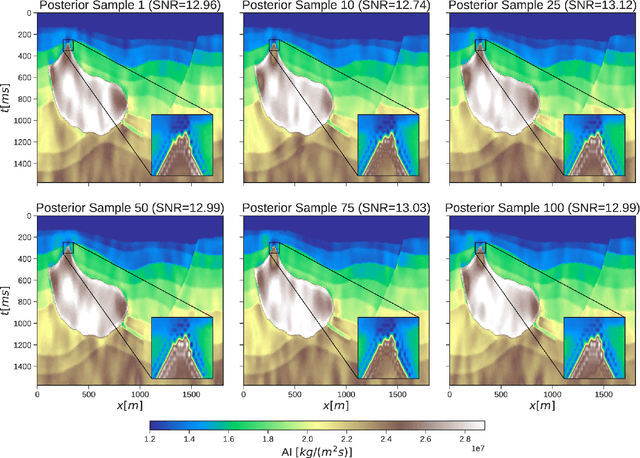
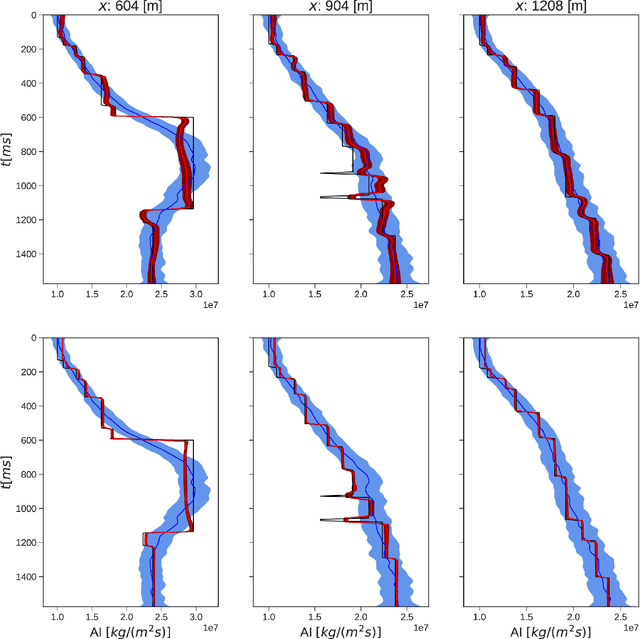
Uncertainty quantification is crucial to inverse problems, as it could provide decision-makers with valuable information about the inversion results. For example, seismic inversion is a notoriously ill-posed inverse problem due to the band-limited and noisy nature of seismic data. It is therefore of paramount importance to quantify the uncertainties associated to the inversion process to ease the subsequent interpretation and decision making processes. Within this framework of reference, sampling from a target posterior provides a fundamental approach to quantifying the uncertainty in seismic inversion. However, selecting appropriate prior information in a probabilistic inversion is crucial, yet non-trivial, as it influences the ability of a sampling-based inference in providing geological realism in the posterior samples. To overcome such limitations, we present a regularized variational inference framework that performs posterior inference by implicitly regularizing the Kullback-Leibler divergence loss with a CNN-based denoiser by means of the Plug-and-Play methods. We call this new algorithm Plug-and-Play Stein Variational Gradient Descent (PnP-SVGD) and demonstrate its ability in producing high-resolution, trustworthy samples representative of the subsurface structures, which we argue could be used for post-inference tasks such as reservoir modelling and history matching. To validate the proposed method, numerical tests are performed on both synthetic and field post-stack seismic data.

Deep Preconditioners and their application to seismic wavefield processing

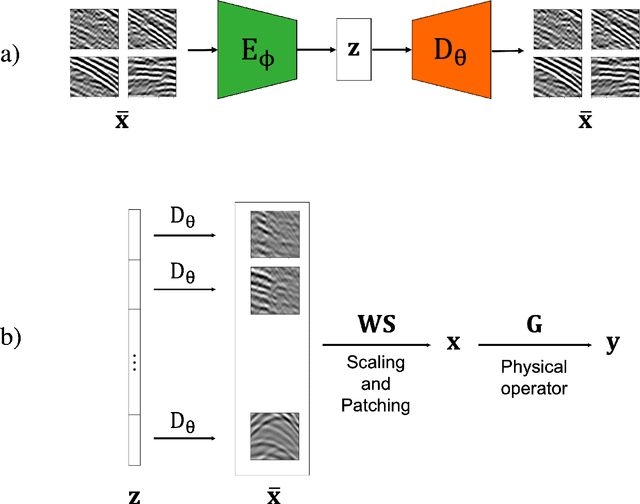
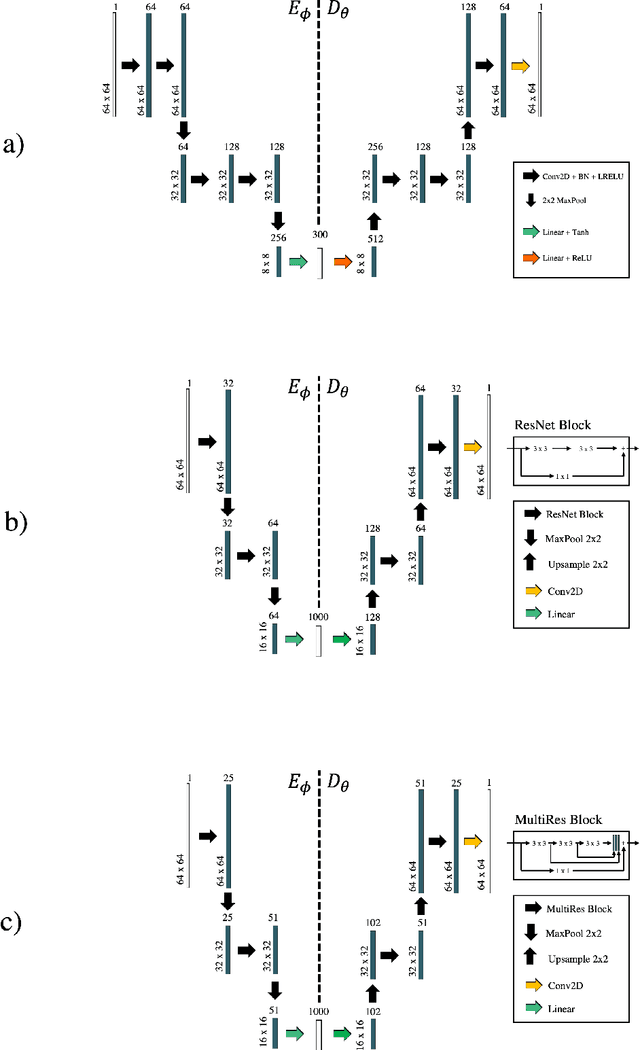
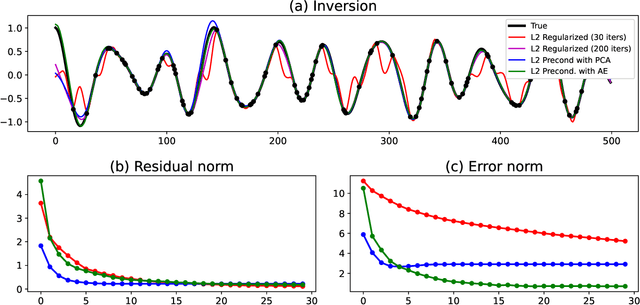
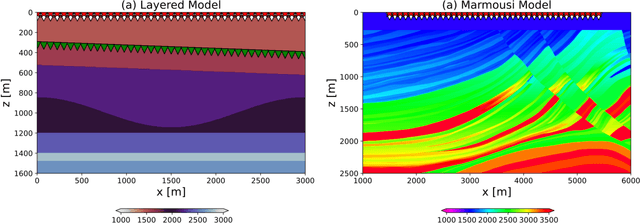
Seismic data processing heavily relies on the solution of physics-driven inverse problems. In the presence of unfavourable data acquisition conditions (e.g., regular or irregular coarse sampling of sources and/or receivers), the underlying inverse problem becomes very ill-posed and prior information is required to obtain a satisfactory solution. Sparsity-promoting inversion, coupled with fixed-basis sparsifying transforms, represent the go-to approach for many processing tasks due to its simplicity of implementation and proven successful application in a variety of acquisition scenarios. Leveraging the ability of deep neural networks to find compact representations of complex, multi-dimensional vector spaces, we propose to train an AutoEncoder network to learn a direct mapping between the input seismic data and a representative latent manifold. The trained decoder is subsequently used as a nonlinear preconditioner for the physics-driven inverse problem at hand. Synthetic and field data are presented for a variety of seismic processing tasks and the proposed nonlinear, learned transformations are shown to outperform fixed-basis transforms and convergence faster to the sought solution.

A hybrid approach to seismic deblending: when physics meets self-supervision

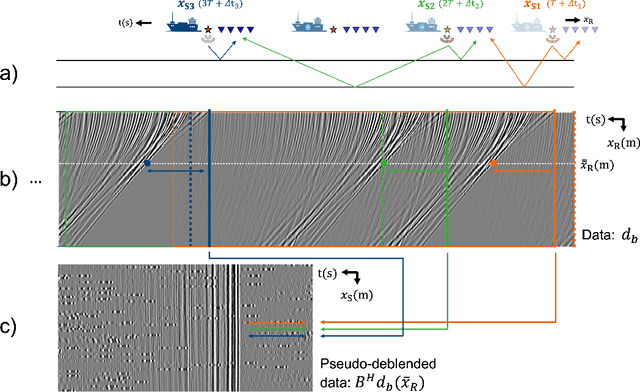
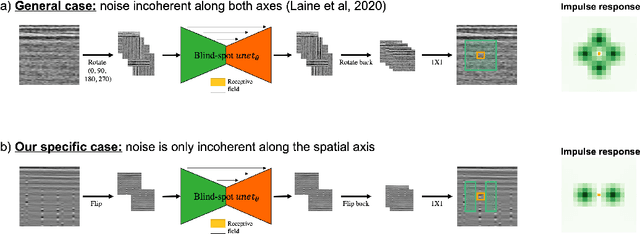
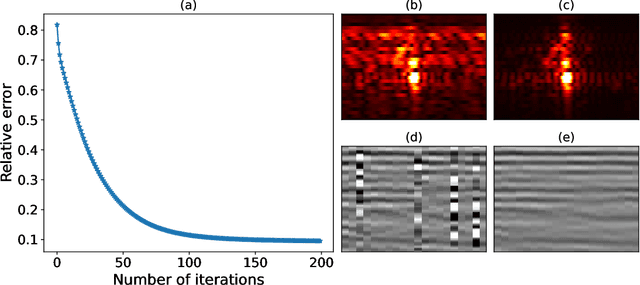
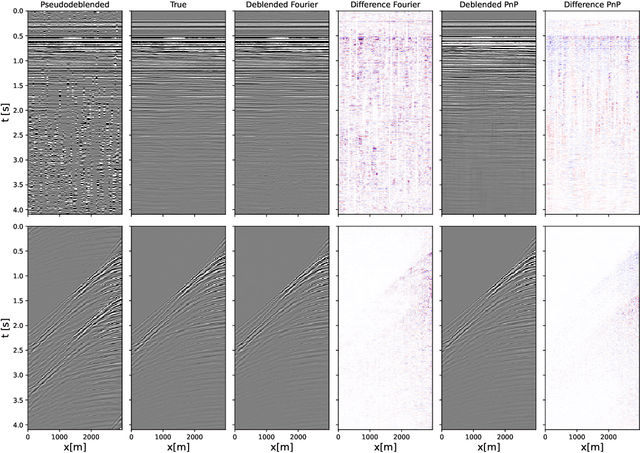
To limit the time, cost, and environmental impact associated with the acquisition of seismic data, in recent decades considerable effort has been put into so-called simultaneous shooting acquisitions, where seismic sources are fired at short time intervals between each other. As a consequence, waves originating from consecutive shots are entangled within the seismic recordings, yielding so-called blended data. For processing and imaging purposes, the data generated by each individual shot must be retrieved. This process, called deblending, is achieved by solving an inverse problem which is heavily underdetermined. Conventional approaches rely on transformations that render the blending noise into burst-like noise, whilst preserving the signal of interest. Compressed sensing type regularization is then applied, where sparsity in some domain is assumed for the signal of interest. The domain of choice depends on the geometry of the acquisition and the properties of seismic data within the chosen domain. In this work, we introduce a new concept that consists of embedding a self-supervised denoising network into the Plug-and-Play (PnP) framework. A novel network is introduced whose design extends the blind-spot network architecture of [28 ] for partially coherent noise (i.e., correlated in time). The network is then trained directly on the noisy input data at each step of the PnP algorithm. By leveraging both the underlying physics of the problem and the great denoising capabilities of our blind-spot network, the proposed algorithm is shown to outperform an industry-standard method whilst being comparable in terms of computational cost. Moreover, being independent on the acquisition geometry, our method can be easily applied to both marine and land data without any significant modification.

The potential of self-supervised networks for random noise suppression in seismic data

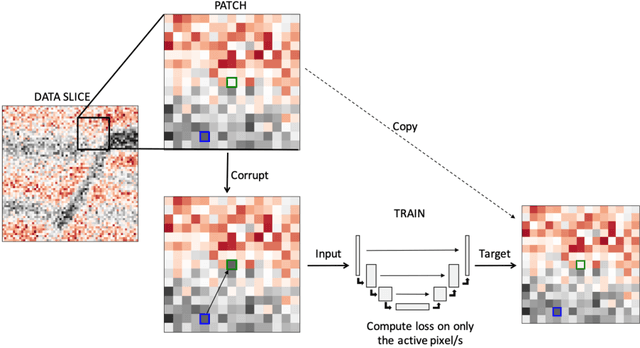
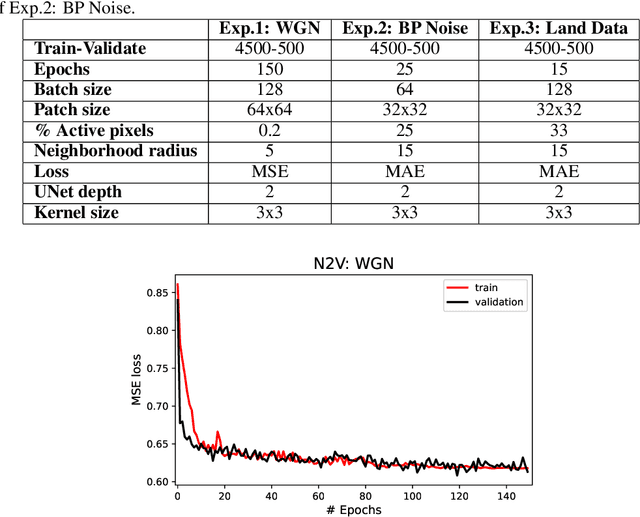
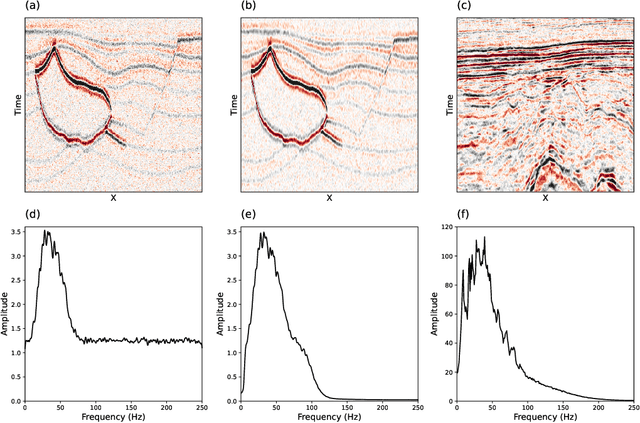
Noise suppression is an essential step in any seismic processing workflow. A portion of this noise, particularly in land datasets, presents itself as random noise. In recent years, neural networks have been successfully used to denoise seismic data in a supervised fashion. However, supervised learning always comes with the often unachievable requirement of having noisy-clean data pairs for training. Using blind-spot networks, we redefine the denoising task as a self-supervised procedure where the network uses the surrounding noisy samples to estimate the noise-free value of a central sample. Based on the assumption that noise is statistically independent between samples, the network struggles to predict the noise component of the sample due to its randomnicity, whilst the signal component is accurately predicted due to its spatio-temporal coherency. Illustrated on synthetic examples, the blind-spot network is shown to be an efficient denoiser of seismic data contaminated by random noise with minimal damage to the signal; therefore, providing improvements in both the image domain and down-the-line tasks, such as inversion. To conclude the study, the suggested approach is applied to field data and the results are compared with two commonly used random denoising techniques: FX-deconvolution and Curvelet transform. By demonstrating that blind-spot networks are an efficient suppressor of random noise, we believe this is just the beginning of utilising self-supervised learning in seismic applications.