PINNslope: seismic data interpolation and local slope estimation with physics informed neural networks
Paper and Code
May 25, 2023
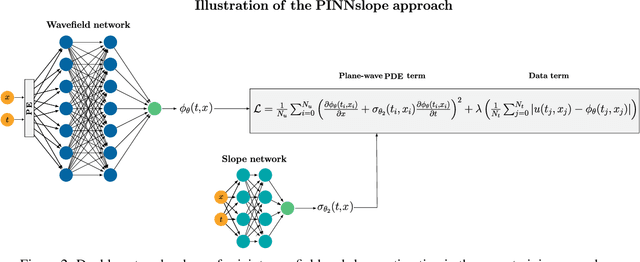
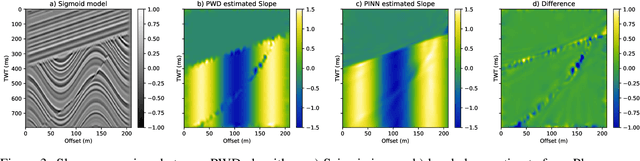
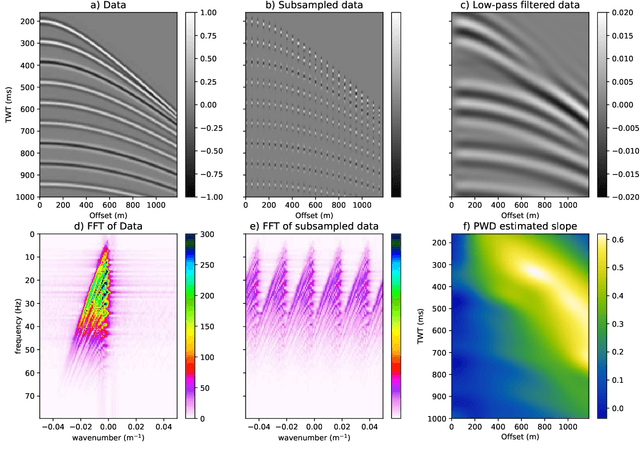
Interpolation of aliased seismic data constitutes a key step in a seismic processing workflow to obtain high quality velocity models and seismic images. Leveraging on the idea of describing seismic wavefields as a superposition of local plane waves, we propose to interpolate seismic data by utilizing a physics informed neural network (PINN). In the proposed framework, two feed-forward neural networks are jointly trained using the local plane wave differential equation as well as the available data as two terms in the objective function: a primary network assisted by positional encoding is tasked with reconstructing the seismic data, whilst an auxiliary, smaller network estimates the associated local slopes. Results on synthetic and field data validate the effectiveness of the proposed method in handling aliased (sampled coarsely) data and data with large gaps. Our method compares favorably against a classic least-squares inversion approach regularized by the local plane-wave equation as well as a PINN-based approach with a single network and pre-computed local slopes. We find that by introducing a second network to estimate the local slopes whilst at the same time interpolating the aliased data, the overall reconstruction capabilities and convergence behavior of the primary network is enhanced. An additional positional encoding, embedded as a network layer, confers to the network the ability to converge faster improving the accuracy of the data term.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge