IntraSeismic: a coordinate-based learning approach to seismic inversion

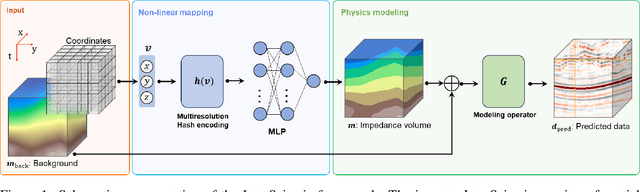
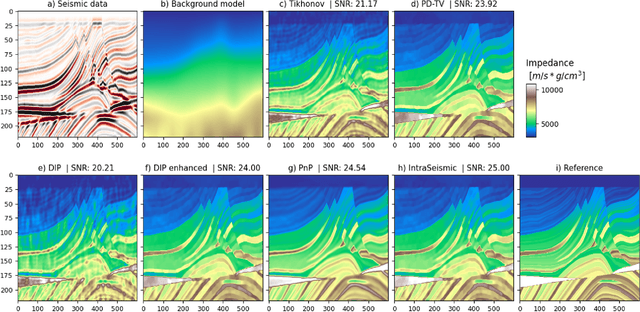
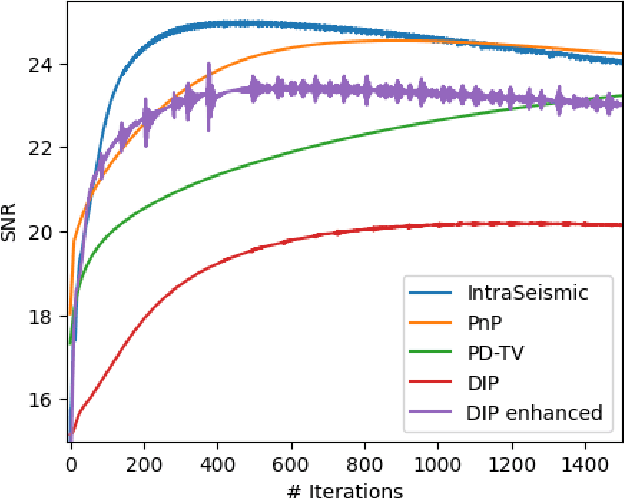
Seismic imaging is the numerical process of creating a volumetric representation of the subsurface geological structures from elastic waves recorded at the surface of the Earth. As such, it is widely utilized in the energy and construction sectors for applications ranging from oil and gas prospection, to geothermal production and carbon capture and storage monitoring, to geotechnical assessment of infrastructures. Extracting quantitative information from seismic recordings, such as an acoustic impedance model, is however a highly ill-posed inverse problem, due to the band-limited and noisy nature of the data. This paper introduces IntraSeismic, a novel hybrid seismic inversion method that seamlessly combines coordinate-based learning with the physics of the post-stack modeling operator. Key features of IntraSeismic are i) unparalleled performance in 2D and 3D post-stack seismic inversion, ii) rapid convergence rates, iii) ability to seamlessly include hard constraints (i.e., well data) and perform uncertainty quantification, and iv) potential data compression and fast randomized access to portions of the inverted model. Synthetic and field data applications of IntraSeismic are presented to validate the effectiveness of the proposed method.

Posterior sampling with CNN-based, Plug-and-Play regularization with applications to Post-Stack Seismic Inversion

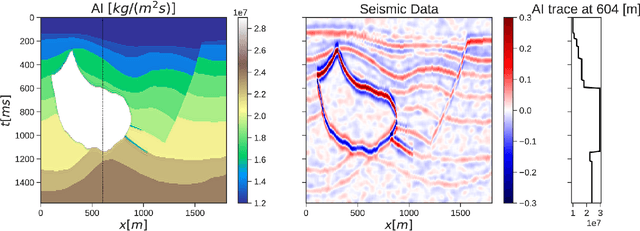
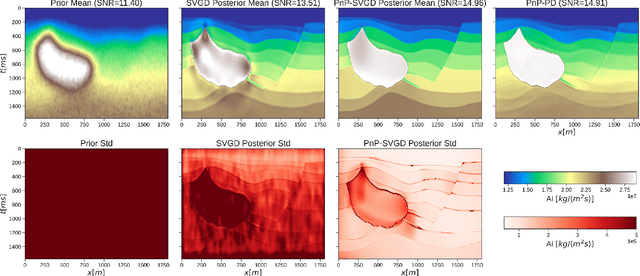
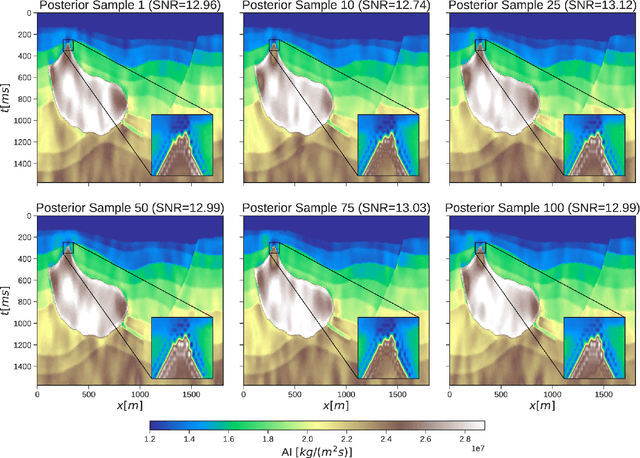
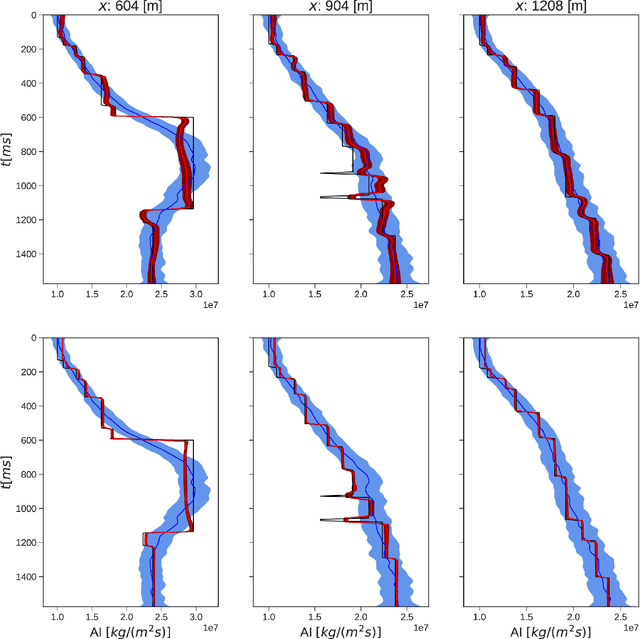
Uncertainty quantification is crucial to inverse problems, as it could provide decision-makers with valuable information about the inversion results. For example, seismic inversion is a notoriously ill-posed inverse problem due to the band-limited and noisy nature of seismic data. It is therefore of paramount importance to quantify the uncertainties associated to the inversion process to ease the subsequent interpretation and decision making processes. Within this framework of reference, sampling from a target posterior provides a fundamental approach to quantifying the uncertainty in seismic inversion. However, selecting appropriate prior information in a probabilistic inversion is crucial, yet non-trivial, as it influences the ability of a sampling-based inference in providing geological realism in the posterior samples. To overcome such limitations, we present a regularized variational inference framework that performs posterior inference by implicitly regularizing the Kullback-Leibler divergence loss with a CNN-based denoiser by means of the Plug-and-Play methods. We call this new algorithm Plug-and-Play Stein Variational Gradient Descent (PnP-SVGD) and demonstrate its ability in producing high-resolution, trustworthy samples representative of the subsurface structures, which we argue could be used for post-inference tasks such as reservoir modelling and history matching. To validate the proposed method, numerical tests are performed on both synthetic and field post-stack seismic data.

A hybrid approach to seismic deblending: when physics meets self-supervision

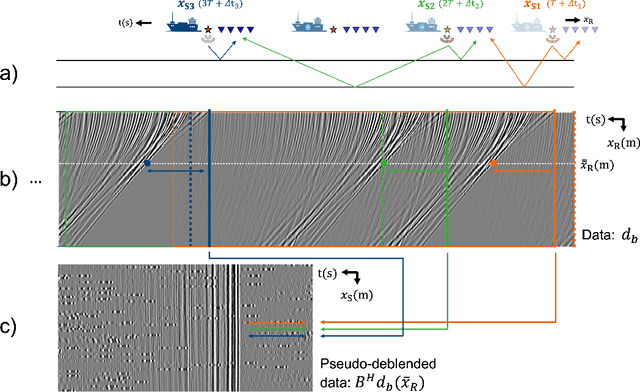
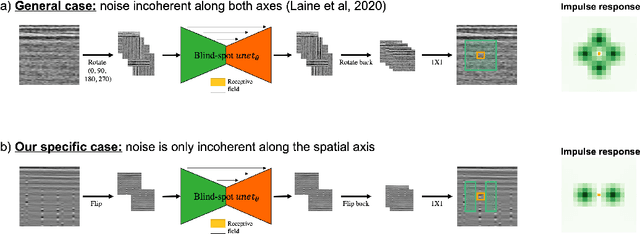
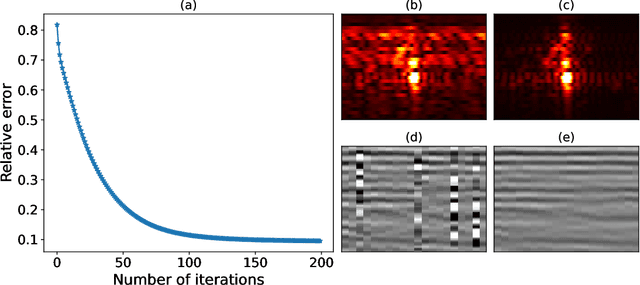
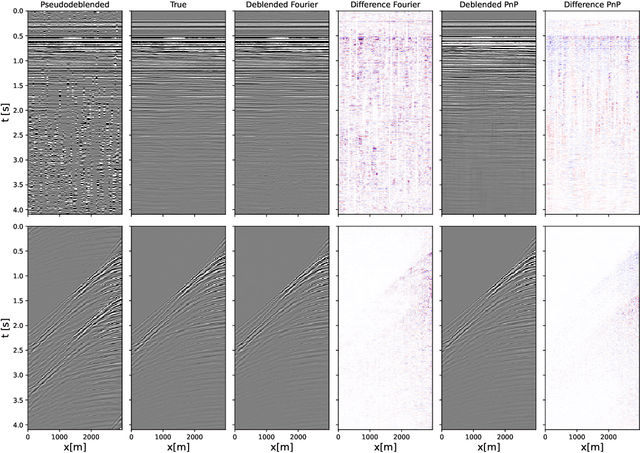
To limit the time, cost, and environmental impact associated with the acquisition of seismic data, in recent decades considerable effort has been put into so-called simultaneous shooting acquisitions, where seismic sources are fired at short time intervals between each other. As a consequence, waves originating from consecutive shots are entangled within the seismic recordings, yielding so-called blended data. For processing and imaging purposes, the data generated by each individual shot must be retrieved. This process, called deblending, is achieved by solving an inverse problem which is heavily underdetermined. Conventional approaches rely on transformations that render the blending noise into burst-like noise, whilst preserving the signal of interest. Compressed sensing type regularization is then applied, where sparsity in some domain is assumed for the signal of interest. The domain of choice depends on the geometry of the acquisition and the properties of seismic data within the chosen domain. In this work, we introduce a new concept that consists of embedding a self-supervised denoising network into the Plug-and-Play (PnP) framework. A novel network is introduced whose design extends the blind-spot network architecture of [28 ] for partially coherent noise (i.e., correlated in time). The network is then trained directly on the noisy input data at each step of the PnP algorithm. By leveraging both the underlying physics of the problem and the great denoising capabilities of our blind-spot network, the proposed algorithm is shown to outperform an industry-standard method whilst being comparable in terms of computational cost. Moreover, being independent on the acquisition geometry, our method can be easily applied to both marine and land data without any significant modification.