Multimodal Medical Disease Classification with LLaMA II

Medical patient data is always multimodal. Images, text, age, gender, histopathological data are only few examples for different modalities in this context. Processing and integrating this multimodal data with deep learning based methods is of utmost interest due to its huge potential for medical procedure such as diagnosis and patient treatment planning. In this work we retrain a multimodal transformer-based model for disease classification. To this end we use the text-image pair dataset from OpenI consisting of 2D chest X-rays associated with clinical reports. Our focus is on fusion methods for merging text and vision information extracted from medical datasets. Different architecture structures with a LLaMA II backbone model are tested. Early fusion of modality specific features creates better results with the best model reaching 97.10% mean AUC than late fusion from a deeper level of the architecture (best model: 96.67% mean AUC). Both outperform former classification models tested on the same multimodal dataset. The newly introduced multimodal architecture can be applied to other multimodal datasets with little effort and can be easily adapted for further research, especially, but not limited to, the field of medical AI.

Matrix-Valued LogSumExp Approximation for Colour Morphology

Mathematical morphology is a part of image processing that uses a window that moves across the image to change certain pixels according to certain operations. The concepts of supremum and infimum play a crucial role here, but it proves challenging to define them generally for higher-dimensional data, such as colour representations. Numerous approaches have therefore been taken to solve this problem with certain compromises. In this paper we will analyse the construction of a new approach, which we have already presented experimentally in paper [Kahra, M., Breu{\ss}, M., Kleefeld, A., Welk, M., DGMM 2024, pp. 325-337]. This is based on a method by Burgeth and Kleefeld [Burgeth, B., Kleefeld, A., ISMM 2013, pp. 243-254], who regard the colours as symmetric $2\times2$ matrices and compare them by means of the Loewner order in a bi-cone through different suprema. However, we will replace the supremum with the LogExp approximation for the maximum instead. This allows us to transfer the associativity of the dilation from the one-dimensional case to the higher-dimensional case. In addition, we will investigate the minimality property and specify a relaxation to ensure that our approach is continuously dependent on the input data.

An Approach to Colour Morphological Supremum Formation using the LogSumExp Approximation

Mathematical morphology is a part of image processing that has proven to be fruitful for numerous applications. Two main operations in mathematical morphology are dilation and erosion. These are based on the construction of a supremum or infimum with respect to an order over the tonal range in a certain section of the image. The tonal ordering can easily be realised in grey-scale morphology, and some morphological methods have been proposed for colour morphology. However, all of these have certain limitations. In this paper we present a novel approach to colour morphology extending upon previous work in the field based on the Loewner order. We propose to consider an approximation of the supremum by means of a log-sum exponentiation introduced by Maslov. We apply this to the embedding of an RGB image in a field of symmetric $2\times2$ matrices. In this way we obtain nearly isotropic matrices representing colours and the structural advantage of transitivity. In numerical experiments we highlight some remarkable properties of the proposed approach.

Tackling the Class Imbalance Problem of Deep Learning Based Head and Neck Organ Segmentation

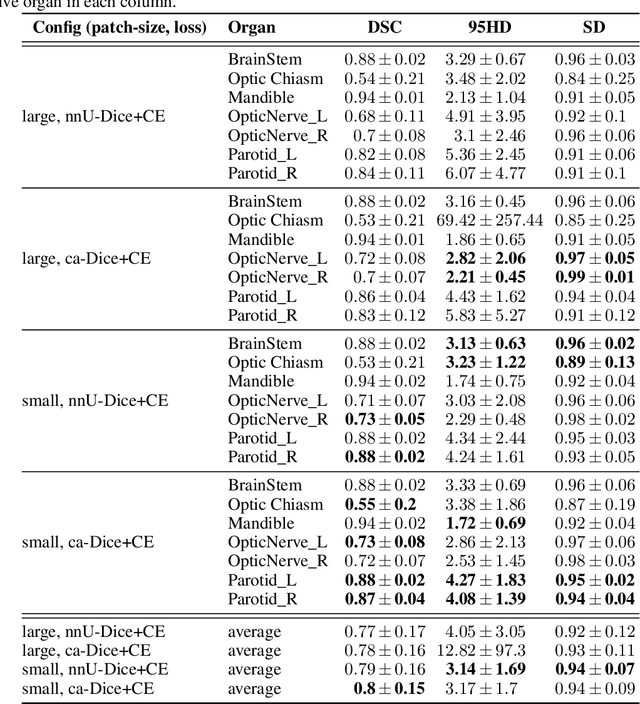
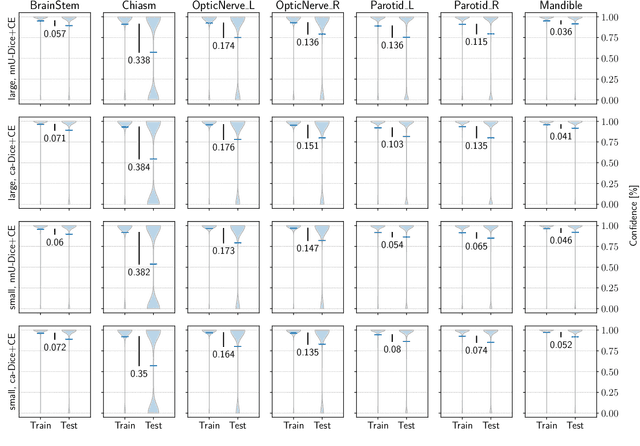
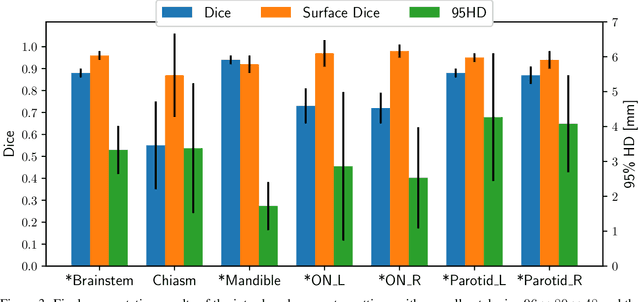
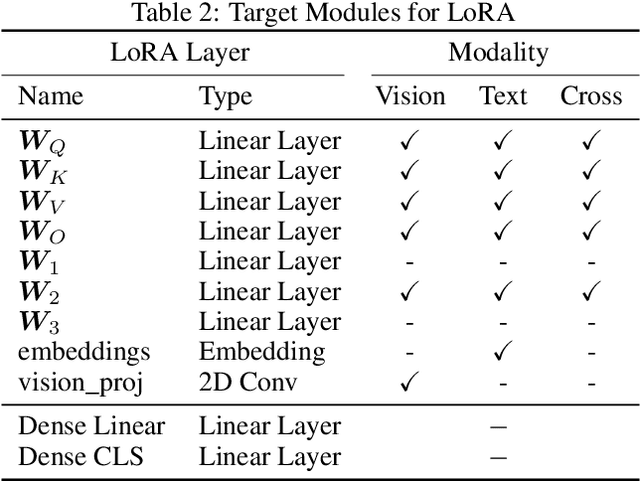
The segmentation of organs at risk (OAR) is a required precondition for the cancer treatment with image guided radiation therapy. The automation of the segmentation task is therefore of high clinical relevance. Deep Learning (DL) based medical image segmentation is currently the most successful approach, but suffers from the over-presence of the background class and the anatomically given organ size difference, which is most severe in the head and neck (HAN) area. To tackle the HAN area specific class imbalance problem we first optimize the patch-size of the currently best performing general purpose segmentation framework, the nnU-Net, based on the introduced class imbalance measurement, and second, introduce the class adaptive Dice loss to further compensate for the highly imbalanced setting. Both the patch-size and the loss function are parameters with direct influence on the class imbalance and their optimization leads to a 3\% increase of the Dice score and 22% reduction of the 95% Hausdorff distance compared to the baseline, finally reaching $0.8\pm0.15$ and $3.17\pm1.7$ mm for the segmentation of seven HAN organs using a single and simple neural network. The patch-size optimization and the class adaptive Dice loss are both simply integrable in current DL based segmentation approaches and allow to increase the performance for class imbalanced segmentation tasks.

Multivariate Medians for Image and Shape Analysis

Having been studied since long by statisticians, multivariate median concepts found their way into the image processing literature in the course of the last decades, being used to construct robust and efficient denoising filters for multivariate images such as colour images but also matrix-valued images. Based on the similarities between image and geometric data as results of the sampling of continuous physical quantities, it can be expected that the understanding of multivariate median filters for images provides a starting point for the development of shape processing techniques. This paper presents an overview of multivariate median concepts relevant for image and shape processing. It focusses on their mathematical principles and discusses important properties especially in the context of image processing.

Stable Backward Diffusion Models that Minimise Convex Energies

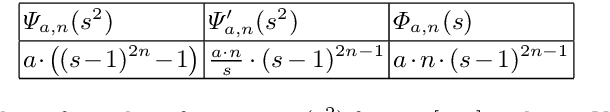
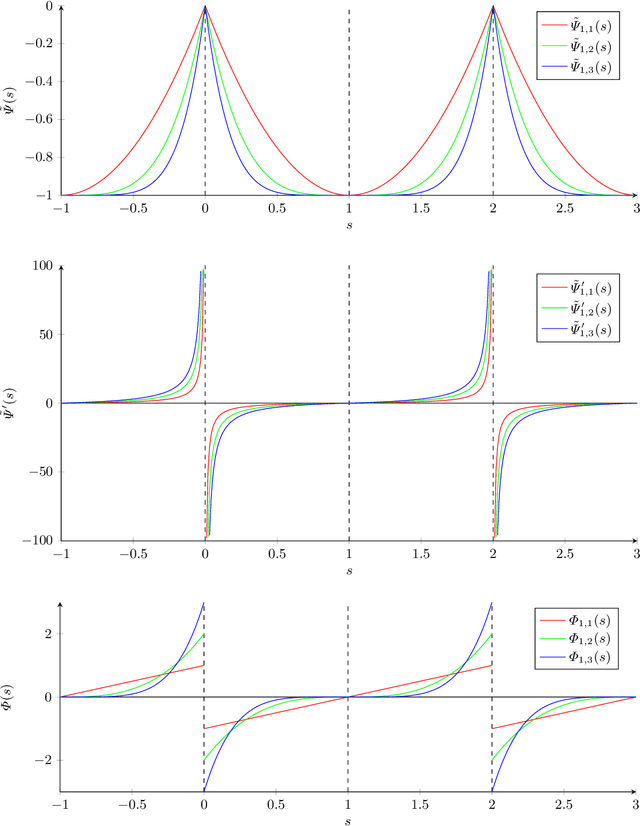
Backward diffusion processes appear naturally in image enhancement and deblurring applications. However, the inverse problem of backward diffusion is known to be ill-posed and straightforward numerical algorithms are unstable. So far, existing stabilisation strategies in the literature require sophisticated numerics to solve the underlying initial value problem. Therefore, it is desirable to establish a backward diffusion model which implements a smart stabilisation approach that can be used in combination with a simple numerical scheme. We derive a class of space-discrete one-dimensional backward diffusion as gradient descent of energies where we gain stability by imposing range constraints. Interestingly, these energies are even convex. Furthermore, we establish a comprehensive theory for the time-continuous evolution and we show that stability carries over to a simple explicit time discretisation of our model. Finally, we confirm the stability and usefulness of our technique in experiments in which we enhance the contrast of digital greyscale and colour images.

Multivariate Median Filters and Partial Differential Equations

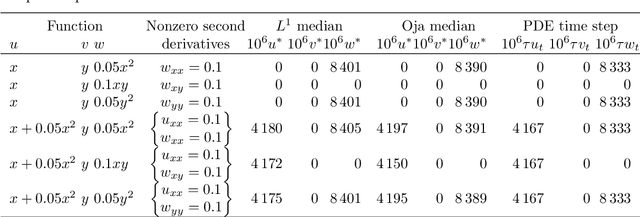
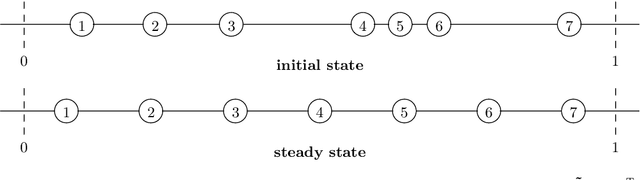
Multivariate median filters have been proposed as generalisations of the well-established median filter for grey-value images to multi-channel images. As multivariate median, most of the recent approaches use the $L^1$ median, i.e.\ the minimiser of an objective function that is the sum of distances to all input points. Many properties of univariate median filters generalise to such a filter. However, the famous result by Guichard and Morel about approximation of the mean curvature motion PDE by median filtering does not have a comparably simple counterpart for $L^1$ multivariate median filtering. We discuss the affine equivariant Oja median and the affine equivariant transformation--retransformation $L^1$ median as alternatives to $L^1$ median filtering. We analyse multivariate median filters in a space-continuous setting, including the formulation of a space-continuous version of the transformation--retransformation $L^1$ median, and derive PDEs approximated by these filters in the cases of bivariate planar images, three-channel volume images and three-channel planar images. The PDEs for the affine equivariant filters can be interpreted geometrically as combinations of a diffusion and a principal-component-wise curvature motion contribution with a cross-effect term based on torsions of principal components. Numerical experiments are presented that demonstrate the validity of the approximation results.

Graph entropies in texture segmentation of images

We study the applicability of a set of texture descriptors introduced in recent work by the author to texture-based segmentation of images. The texture descriptors under investigation result from applying graph indices from quantitative graph theory to graphs encoding the local structure of images. The underlying graphs arise from the computation of morphological amoebas as structuring elements for adaptive morphology, either as weighted or unweighted Dijkstra search trees or as edge-weighted pixel graphs within structuring elements. In the present paper we focus on texture descriptors in which the graph indices are entropy-based, and use them in a geodesic active contour framework for image segmentation. Experiments on several synthetic and one real-world image are shown to demonstrate texture segmentation by this approach. Forthermore, we undertake an attempt to analyse selected entropy-based texture descriptors with regard to what information about texture they actually encode. Whereas this analysis uses some heuristic assumptions, it indicates that the graph-based texture descriptors are related to fractal dimension measures that have been proven useful in texture analysis.

Amoeba Techniques for Shape and Texture Analysis

Morphological amoebas are image-adaptive structuring elements for morphological and other local image filters introduced by Lerallut et al. Their construction is based on combining spatial distance with contrast information into an image-dependent metric. Amoeba filters show interesting parallels to image filtering methods based on partial differential equations (PDEs), which can be confirmed by asymptotic equivalence results. In computing amoebas, graph structures are generated that hold information about local image texture. This paper reviews and summarises the work of the author and his coauthors on morphological amoebas, particularly their relations to PDE filters and texture analysis. It presents some extensions and points out directions for future investigation on the subject.

Analysis of Amoeba Active Contours

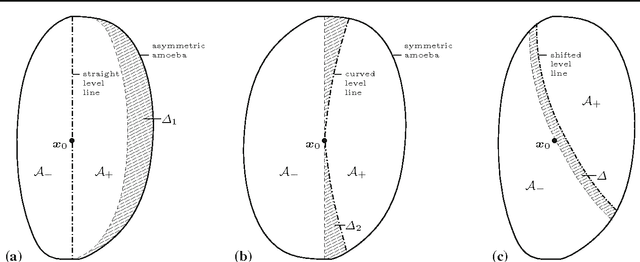
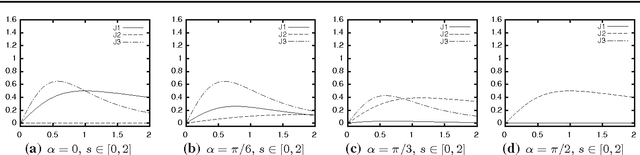
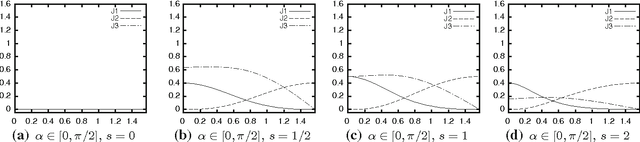
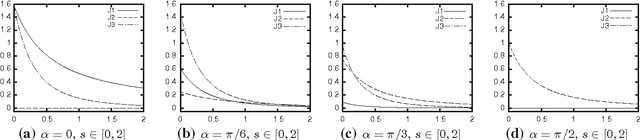
Subject of this paper is the theoretical analysis of structure-adaptive median filter algorithms that approximate curvature-based PDEs for image filtering and segmentation. These so-called morphological amoeba filters are based on a concept introduced by Lerallut et al. They achieve similar results as the well-known geodesic active contour and self-snakes PDEs. In the present work, the PDE approximated by amoeba active contours is derived for a general geometric situation and general amoeba metric. This PDE is structurally similar but not identical to the geodesic active contour equation. It reproduces the previous PDE approximation results for amoeba median filters as special cases. Furthermore, modifications of the basic amoeba active contour algorithm are analysed that are related to the morphological force terms frequently used with geodesic active contours. Experiments demonstrate the basic behaviour of amoeba active contours and its similarity to geodesic active contours.