Analysis of Amoeba Active Contours
Paper and Code
Jul 12, 2014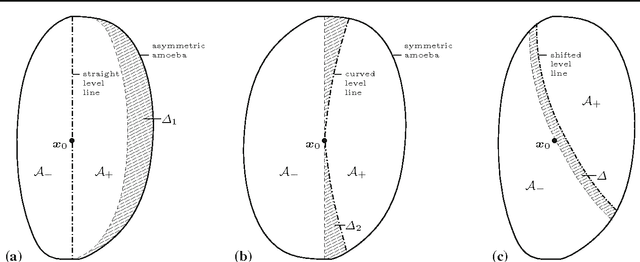
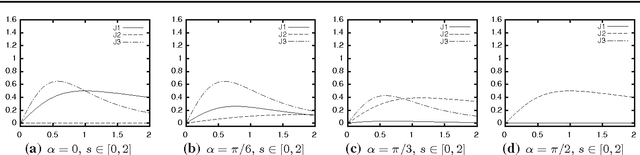
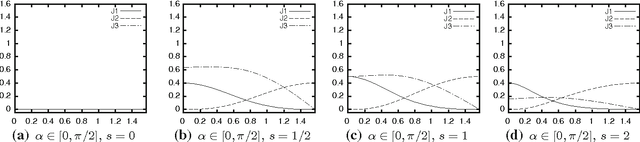
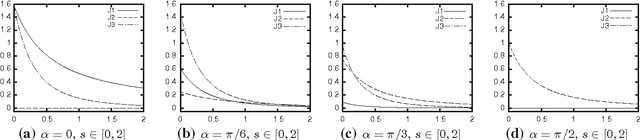
Subject of this paper is the theoretical analysis of structure-adaptive median filter algorithms that approximate curvature-based PDEs for image filtering and segmentation. These so-called morphological amoeba filters are based on a concept introduced by Lerallut et al. They achieve similar results as the well-known geodesic active contour and self-snakes PDEs. In the present work, the PDE approximated by amoeba active contours is derived for a general geometric situation and general amoeba metric. This PDE is structurally similar but not identical to the geodesic active contour equation. It reproduces the previous PDE approximation results for amoeba median filters as special cases. Furthermore, modifications of the basic amoeba active contour algorithm are analysed that are related to the morphological force terms frequently used with geodesic active contours. Experiments demonstrate the basic behaviour of amoeba active contours and its similarity to geodesic active contours.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge