Multivariate Median Filters and Partial Differential Equations
Paper and Code
Mar 18, 2016

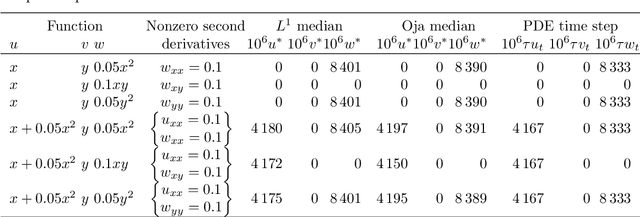

Multivariate median filters have been proposed as generalisations of the well-established median filter for grey-value images to multi-channel images. As multivariate median, most of the recent approaches use the $L^1$ median, i.e.\ the minimiser of an objective function that is the sum of distances to all input points. Many properties of univariate median filters generalise to such a filter. However, the famous result by Guichard and Morel about approximation of the mean curvature motion PDE by median filtering does not have a comparably simple counterpart for $L^1$ multivariate median filtering. We discuss the affine equivariant Oja median and the affine equivariant transformation--retransformation $L^1$ median as alternatives to $L^1$ median filtering. We analyse multivariate median filters in a space-continuous setting, including the formulation of a space-continuous version of the transformation--retransformation $L^1$ median, and derive PDEs approximated by these filters in the cases of bivariate planar images, three-channel volume images and three-channel planar images. The PDEs for the affine equivariant filters can be interpreted geometrically as combinations of a diffusion and a principal-component-wise curvature motion contribution with a cross-effect term based on torsions of principal components. Numerical experiments are presented that demonstrate the validity of the approximation results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge