Heterogeneous Causal Discovery of Repeated Undesirable Health Outcomes

Understanding factors triggering or preventing undesirable health outcomes across patient subpopulations is essential for designing targeted interventions. While randomized controlled trials and expert-led patient interviews are standard methods for identifying these factors, they can be time-consuming and infeasible. Causal discovery offers an alternative to conventional approaches by generating cause-and-effect hypotheses from observational data. However, it often relies on strong or untestable assumptions, which can limit its practical application. This work aims to make causal discovery more practical by considering multiple assumptions and identifying heterogeneous effects. We formulate the problem of discovering causes and effect modifiers of an outcome, where effect modifiers are contexts (e.g., age groups) with heterogeneous causal effects. Then, we present a novel, end-to-end framework that incorporates an ensemble of causal discovery algorithms and estimation of heterogeneous effects to discover causes and effect modifiers that trigger or inhibit the outcome. We demonstrate that the ensemble approach improves robustness by enhancing recall of causal factors while maintaining precision. Our study examines the causes of repeat emergency room visits for diabetic patients and hospital readmissions for ICU patients. Our framework generates causal hypotheses consistent with existing literature and can help practitioners identify potential interventions and patient subpopulations to focus on.

Feature Acquisition using Monte Carlo Tree Search

Feature acquisition algorithms address the problem of acquiring informative features while balancing the costs of acquisition to improve the learning performances of ML models. Previous approaches have focused on calculating the expected utility values of features to determine the acquisition sequences. Other approaches formulated the problem as a Markov Decision Process (MDP) and applied reinforcement learning based algorithms. In comparison to previous approaches, we focus on 1) formulating the feature acquisition problem as a MDP and applying Monte Carlo Tree Search, 2) calculating the intermediary rewards for each acquisition step based on model improvements and acquisition costs and 3) simultaneously optimizing model improvement and acquisition costs with multi-objective Monte Carlo Tree Search. With Proximal Policy Optimization and Deep Q-Network algorithms as benchmark, we show the effectiveness of our proposed approach with experimental study.

Weight Set Decomposition for Weighted Rank Aggregation: An interpretable and visual decision support tool

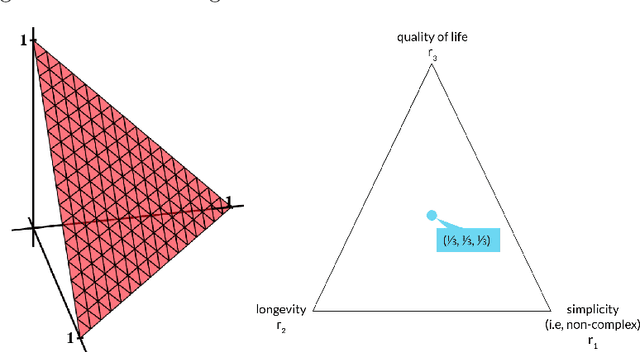
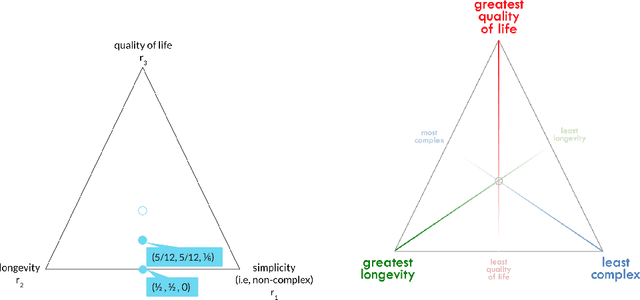
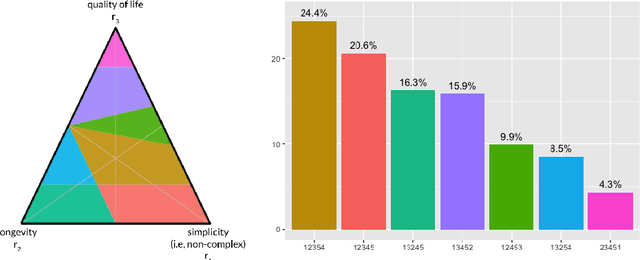
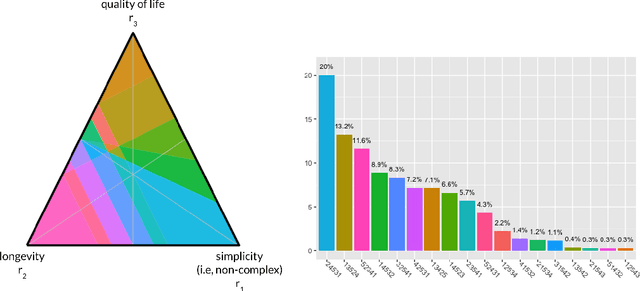
The problem of interpreting or aggregating multiple rankings is common to many real-world applications. Perhaps the simplest and most common approach is a weighted rank aggregation, wherein a (convex) weight is applied to each input ranking and then ordered. This paper describes a new tool for visualizing and displaying ranking information for the weighted rank aggregation method. Traditionally, the aim of rank aggregation is to summarize the information from the input rankings and provide one final ranking that hopefully represents a more accurate or truthful result than any one input ranking. While such an aggregated ranking is, and clearly has been, useful to many applications, it also obscures information. In this paper, we show the wealth of information that is available for the weighted rank aggregation problem due to its structure. We apply weight set decomposition to the set of convex multipliers, study the properties useful for understanding this decomposition, and visualize the indifference regions. This methodology reveals information--that is otherwise collapsed by the aggregated ranking--into a useful, interpretable, and intuitive decision support tool. Included are multiple illustrative examples, along with heuristic and exact algorithms for computing the weight set decomposition.