Scale-out Systolic Arrays

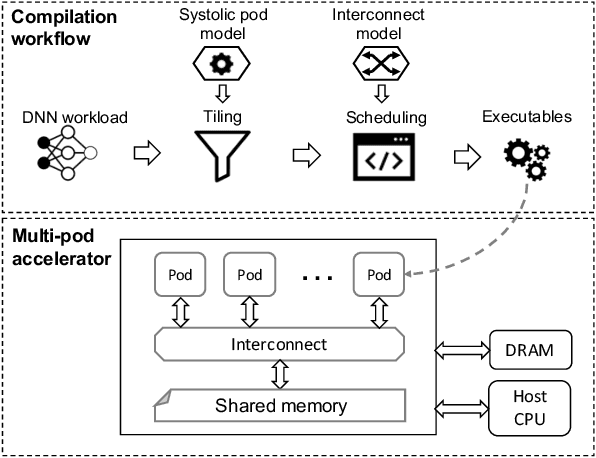
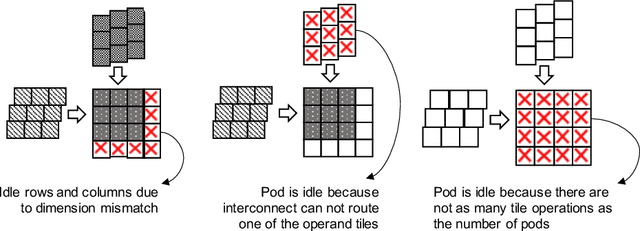
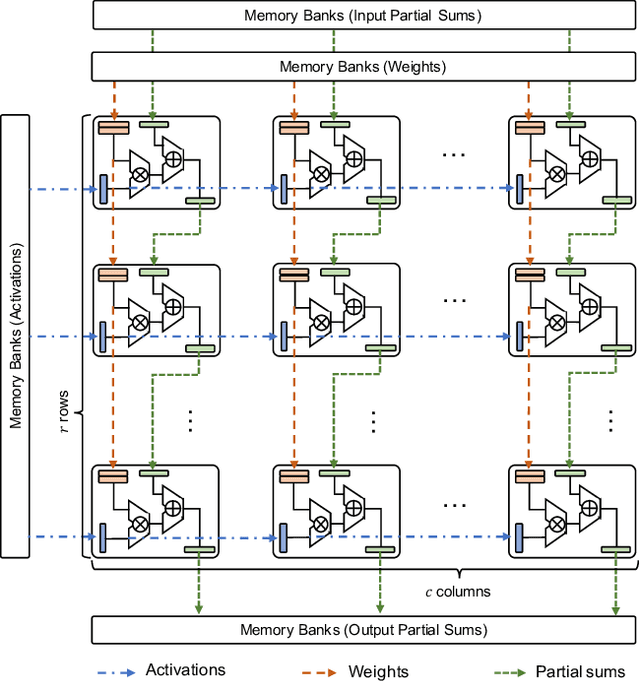
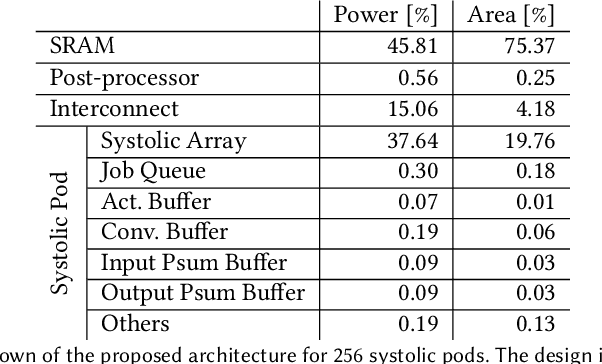
Multi-pod systolic arrays are emerging as the architecture of choice in DNN inference accelerators. Despite their potential, designing multi-pod systolic arrays to maximize effective throughput/Watt (i.e., throughput/Watt adjusted when accounting for array utilization) poses a unique set of challenges. In this work, we study three key pillars in multi-pod systolic array designs, namely array granularity, interconnect, and tiling. We identify optimal array granularity across workloads and show that state-of-the-art commercial accelerators use suboptimal array sizes for single-tenancy workloads. We, then evaluate the bandwidth/latency trade-offs in interconnects and show that Butterfly networks offer a scalable topology for accelerators with a large number of pods. Finally, we introduce a novel data tiling scheme with custom partition size to maximize utilization in optimally sized pods. We propose Scale-out Systolic Arrays, a multi-pod inference accelerator for both single- and multi-tenancy based on these three pillars. We show that SOSA exhibits scaling of up to 600 TeraOps/s in effective throughput for state-of-the-art DNN inference workloads, and outperforms state-of-the-art multi-pod accelerators by a factor of 1.5x.

Training DNNs with Hybrid Block Floating Point

The wide adoption of DNNs has given birth to unrelenting computing requirements, forcing datacenter operators to adopt domain-specific accelerators to train them. These accelerators typically employ densely packed full precision floating-point arithmetic to maximize performance per area. Ongoing research efforts seek to further increase that performance density by replacing floating-point with fixed-point arithmetic. However, a significant roadblock for these attempts has been fixed point's narrow dynamic range, which is insufficient for DNN training convergence. We identify block floating point~(BFP) as a promising alternative representation since it exhibits wide dynamic range and enables the majority of DNN operations to be performed with fixed-point logic. Unfortunately, BFP alone introduces several limitations that preclude its direct applicability. In this work, we introduce HBFP, a hybrid BFP-FP approach, which performs all dot products in BFP and other operations in floating point. HBFP delivers the best of both worlds: the high accuracy of floating point at the superior hardware density of fixed point. For a wide variety of models, we show that HBFP matches floating point's accuracy while enabling hardware implementations that deliver up to 8.5x higher throughput.