Autonomous Driving with a Deep Dual-Model Solution for Steering and Braking Control

The technology of autonomous driving is currently attracting a great deal of interest in both research and industry. In this paper, we present a deep learning dual-model solution that uses two deep neural networks for combined braking and steering in autonomous vehicles. Steering control is achieved by applying the NVIDIA's PilotNet model to predict the steering wheel angle, while braking control relies on the use of MobileNet SSD. Both models rely on a single front-facing camera for image input. The MobileNet SSD model is suitable for devices with constrained resources, whereas PilotNet struggles to operate efficiently on smaller devices with limited resources. To make it suitable for such devices, we modified the PilotNet model using our own original network design and reduced the number of model parameters and its memory footprint by approximately 60%. The inference latency has also been reduced, making the model more suitable to operate on resource-constrained devices. The modified PilotNet model achieves similar loss and accuracy compared to the original PilotNet model. When evaluated in a simulated environment, both autonomous driving systems, one using the modified PilotNet model and the other using the original PilotNet model for steering, show similar levels of autonomous driving performance.

Stochastic Optimization for Trajectory Planning with Heteroscedastic Gaussian Processes

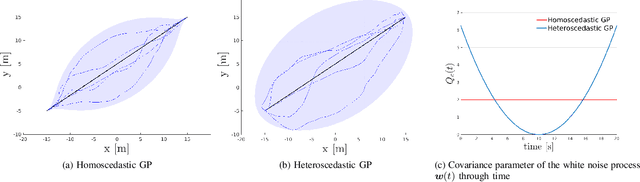
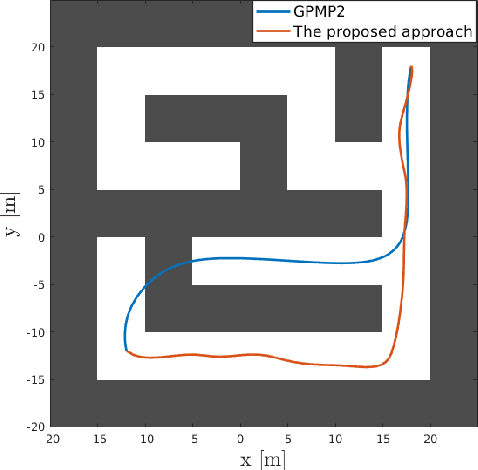
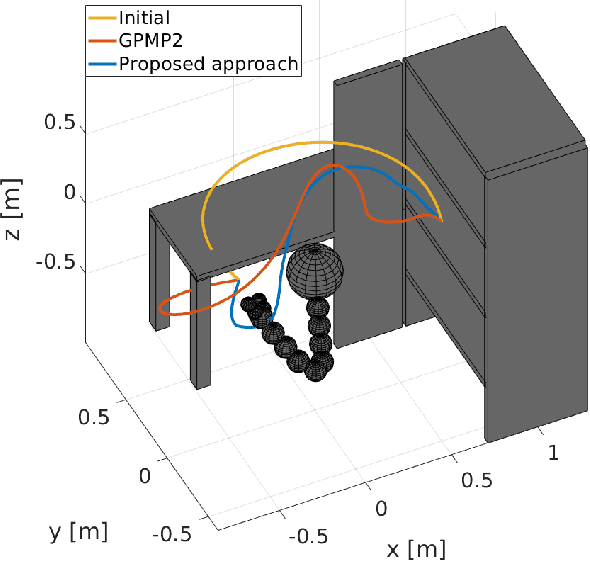
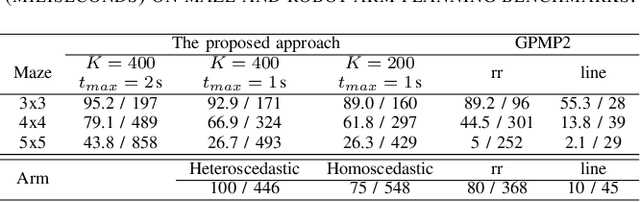
Trajectory optimization methods for motion planning attempt to generate trajectories that minimize a suitable objective function. Such methods efficiently find solutions even for high degree-of-freedom robots. However, a globally optimal solution is often intractable in practice and state-of-the-art trajectory optimization methods are thus prone to local minima, especially in cluttered environments. In this paper, we propose a novel motion planning algorithm that employs stochastic optimization based on the cross-entropy method in order to tackle the local minima problem. We represent trajectories as samples from a continuous-time Gaussian process and introduce heteroscedasticity to generate powerful trajectory priors better suited for collision avoidance in motion planning problems. Our experimental evaluation shows that the proposed approach yields a more thorough exploration of the solution space and a higher success rate in complex environments than a current Gaussian process based state-of-the-art trajectory optimization method, namely GPMP2, while having comparable execution time.

Multi-agent Gaussian Process Motion Planning via Probabilistic Inference

This paper deals with motion planning for multiple agents by representing the problem as a simultaneous optimization of every agent's trajectory. Each trajectory is considered as a sample from a one-dimensional continuous-time Gaussian process (GP) generated by a linear time-varying stochastic differential equation driven by white noise. By formulating the planning problem as probabilistic inference on a factor graph, the structure of the pertaining GP can be exploited to find the solution efficiently using numerical optimization. In contrast to planning each agent's trajectory individually, where only the current poses of other agents are taken into account, we propose simultaneous planning of multiple trajectories that works in a predictive manner. It takes into account the information about each agent's whereabouts at every future time instant, since full trajectories of each agent are found jointly during a single optimization procedure. We compare the proposed method to an individual trajectory planning approach, demonstrating significant improvement in both success rate and computational efficiency.