Multi-agent Gaussian Process Motion Planning via Probabilistic Inference

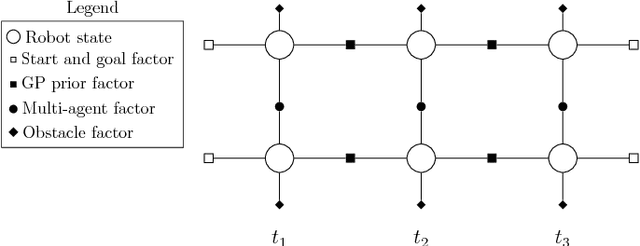
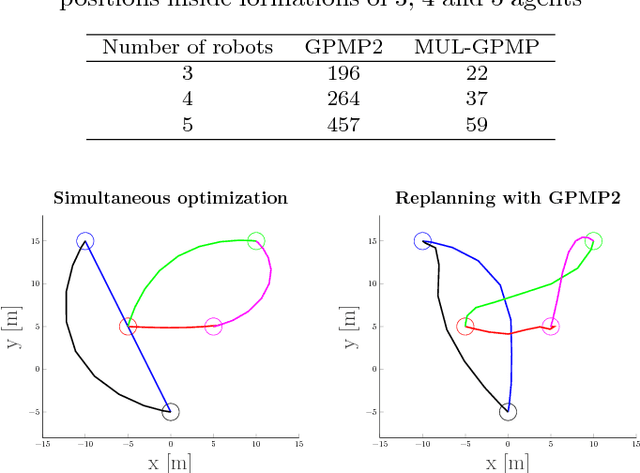
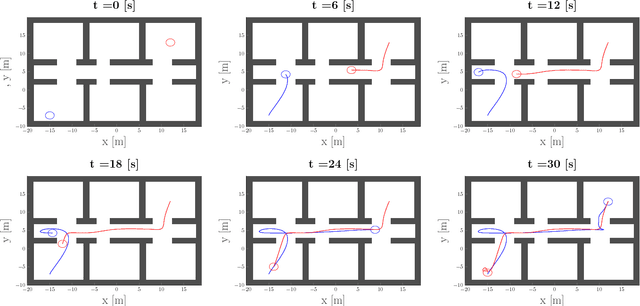
This paper deals with motion planning for multiple agents by representing the problem as a simultaneous optimization of every agent's trajectory. Each trajectory is considered as a sample from a one-dimensional continuous-time Gaussian process (GP) generated by a linear time-varying stochastic differential equation driven by white noise. By formulating the planning problem as probabilistic inference on a factor graph, the structure of the pertaining GP can be exploited to find the solution efficiently using numerical optimization. In contrast to planning each agent's trajectory individually, where only the current poses of other agents are taken into account, we propose simultaneous planning of multiple trajectories that works in a predictive manner. It takes into account the information about each agent's whereabouts at every future time instant, since full trajectories of each agent are found jointly during a single optimization procedure. We compare the proposed method to an individual trajectory planning approach, demonstrating significant improvement in both success rate and computational efficiency.