Stochastic Optimization for Trajectory Planning with Heteroscedastic Gaussian Processes
Paper and Code
Jul 17, 2019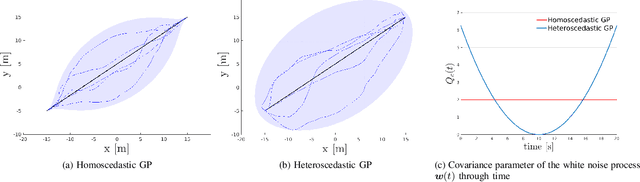
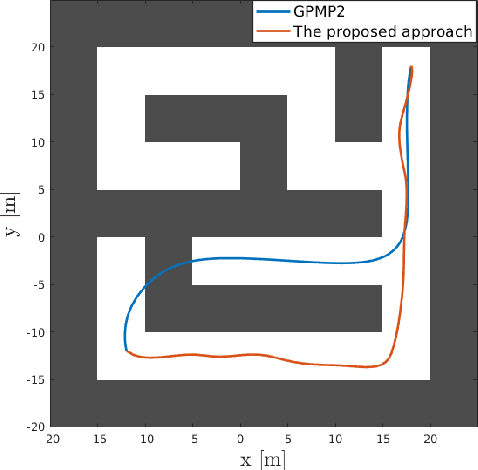
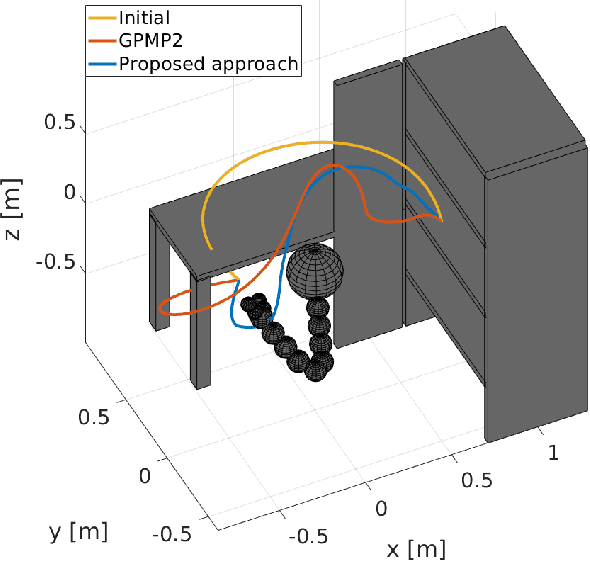
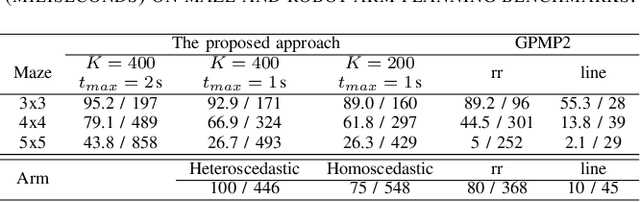
Trajectory optimization methods for motion planning attempt to generate trajectories that minimize a suitable objective function. Such methods efficiently find solutions even for high degree-of-freedom robots. However, a globally optimal solution is often intractable in practice and state-of-the-art trajectory optimization methods are thus prone to local minima, especially in cluttered environments. In this paper, we propose a novel motion planning algorithm that employs stochastic optimization based on the cross-entropy method in order to tackle the local minima problem. We represent trajectories as samples from a continuous-time Gaussian process and introduce heteroscedasticity to generate powerful trajectory priors better suited for collision avoidance in motion planning problems. Our experimental evaluation shows that the proposed approach yields a more thorough exploration of the solution space and a higher success rate in complex environments than a current Gaussian process based state-of-the-art trajectory optimization method, namely GPMP2, while having comparable execution time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge