One Step Preference Elicitation in Multi-Objective Bayesian Optimization

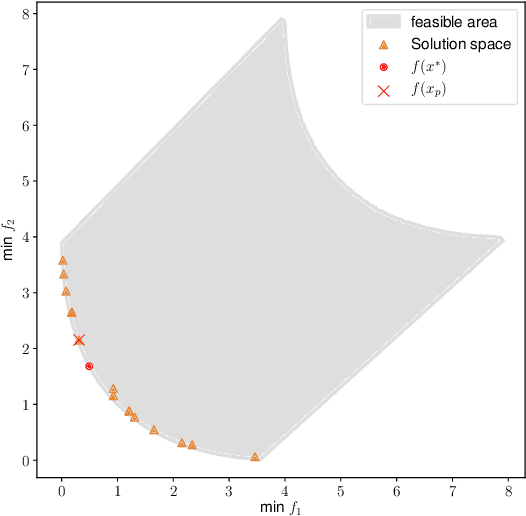
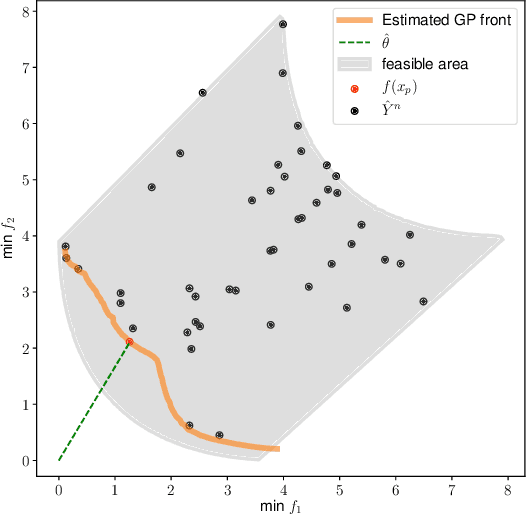
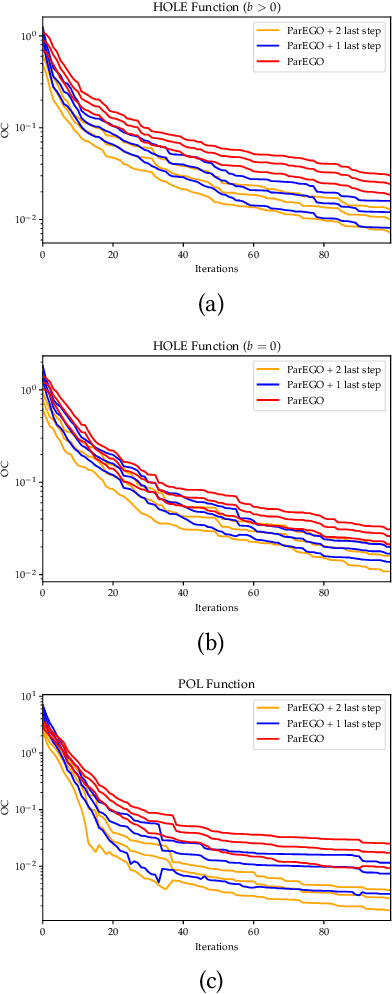
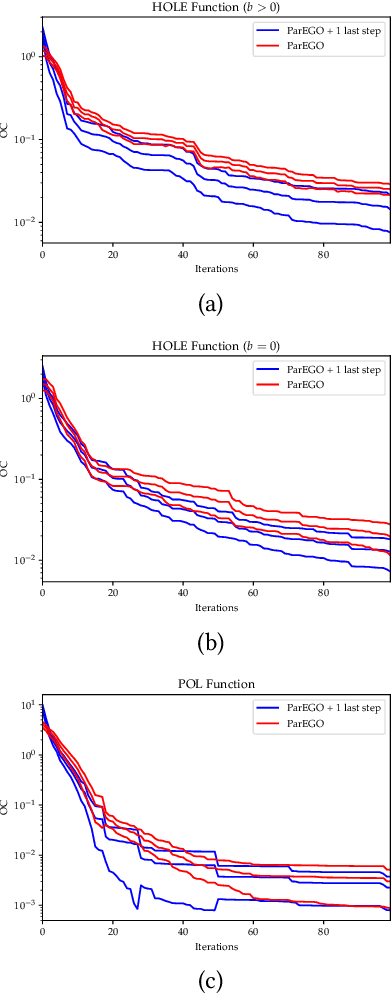
We consider a multi-objective optimization problem with objective functions that are expensive to evaluate. The decision maker (DM) has unknown preferences, and so the standard approach is to generate an approximation of the Pareto front and let the DM choose from the generated non-dominated designs. However, especially for expensive to evaluate problems where the number of designs that can be evaluated is very limited, the true best solution according to the DM's unknown preferences is unlikely to be among the small set of non-dominated solutions found, even if these solutions are truly Pareto optimal. We address this issue by using a multi-objective Bayesian optimization algorithm and allowing the DM to select a preferred solution from a predicted continuous Pareto front just once before the end of the algorithm rather than selecting a solution after the end. This allows the algorithm to understand the DM's preferences and make a final attempt to identify a more preferred solution. We demonstrate the idea using ParEGO, and show empirically that the found solutions are significantly better in terms of true DM preferences than if the DM would simply pick a solution at the end.

Identifying Properties of Real-World Optimisation Problems through a Questionnaire

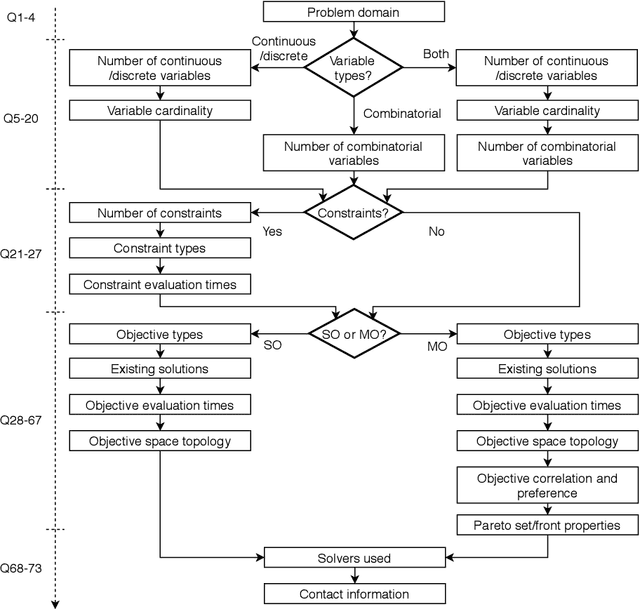
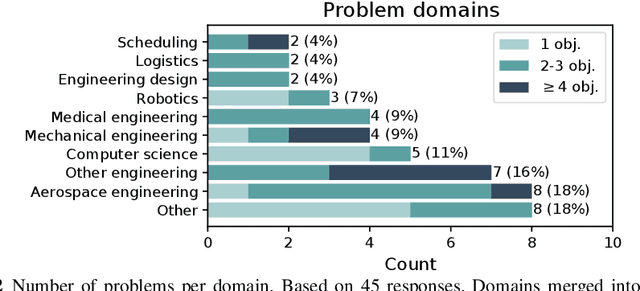
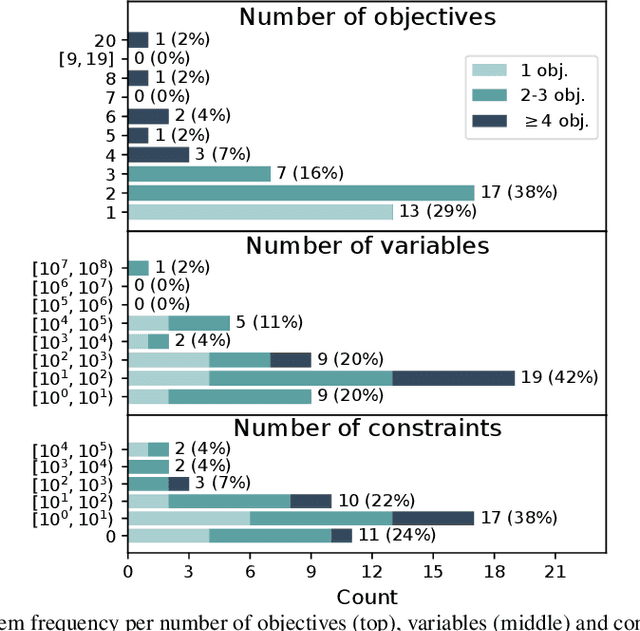
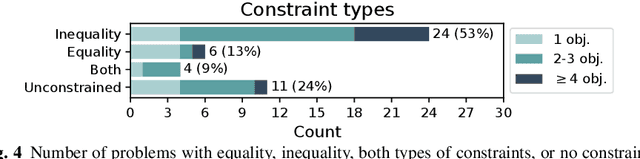
Optimisation algorithms are commonly compared on benchmarks to get insight into performance differences. However, it is not clear how closely benchmarks match the properties of real-world problems because these properties are largely unknown. This work investigates the properties of real-world problems through a questionnaire to enable the design of future benchmark problems that more closely resemble those found in the real world. The results, while not representative, show that many problems possess at least one of the following properties: they are constrained, deterministic, have only continuous variables, require substantial computation times for both the objectives and the constraints, or allow a limited number of evaluations. Properties like known optimal solutions and analytical gradients are rarely available, limiting the options in guiding the optimisation process. These are all important aspects to consider when designing realistic benchmark problems. At the same time, objective functions are often reported to be black-box and since many problem properties are unknown the design of realistic benchmarks is difficult. To further improve the understanding of real-world problems, readers working on a real-world optimisation problem are encouraged to fill out the questionnaire: https://tinyurl.com/opt-survey

Towards Realistic Optimization Benchmarks: A Questionnaire on the Properties of Real-World Problems

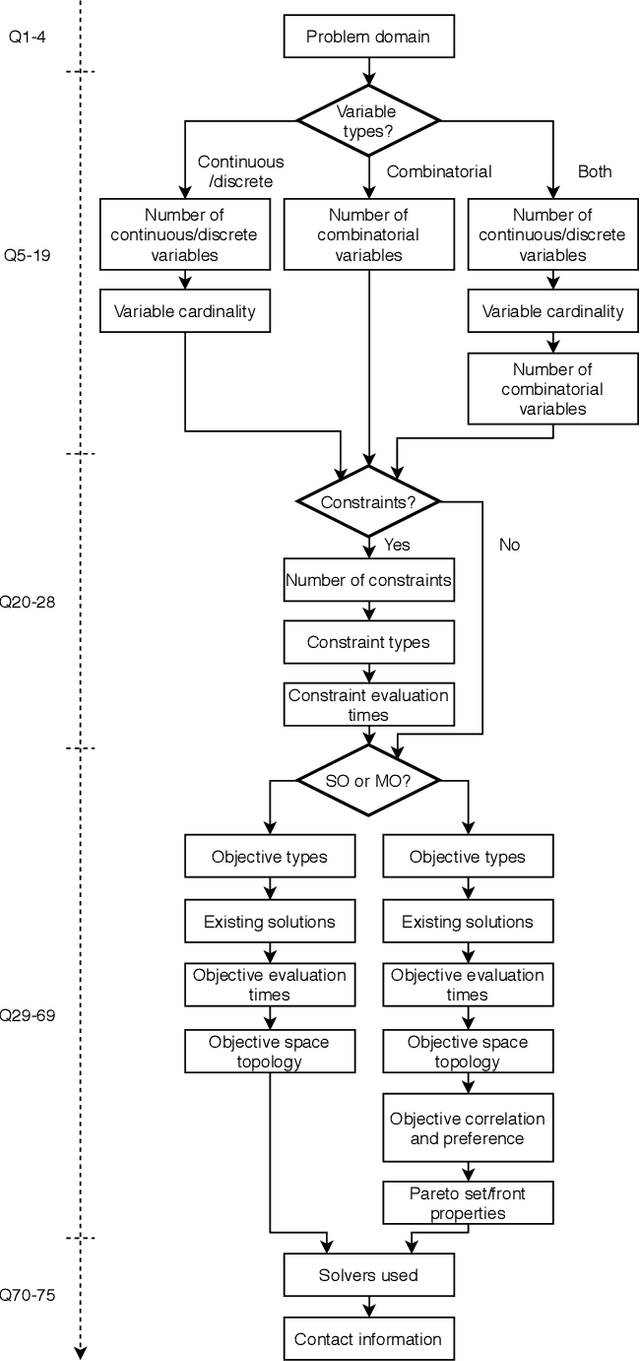
Benchmarks are a useful tool for empirical performance comparisons. However, one of the main shortcomings of existing benchmarks is that it remains largely unclear how they relate to real-world problems. What does an algorithm's performance on a benchmark say about its potential on a specific real-world problem? This work aims to identify properties of real-world problems through a questionnaire on real-world single-, multi-, and many-objective optimization problems. Based on initial responses, a few challenges that have to be considered in the design of realistic benchmarks can already be identified. A key point for future work is to gather more responses to the questionnaire to allow an analysis of common combinations of properties. In turn, such common combinations can then be included in improved benchmark suites. To gather more data, the reader is invited to participate in the questionnaire at: https://tinyurl.com/opt-survey